题目内容
下列四个命题中，不正确的是（ ）A．若函数f（x）在x=x处连续，则
B．函数
的不连续点是x=2和x=-2C．若函数f（x）、g（x）满足
，则
D．
【答案】分析：若函数f（x）、g（x）满足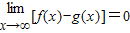
，则
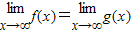不一定成立，因为
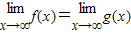成立的前提是
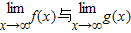必须都存在．故C不正确．
解答：解：A、若函数f（x）在x=x处连续，则f（x）在x=x处有极限，所以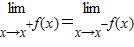
，故A正确．
B、函数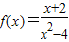
的定义域是{x|x≠±2}，所以它的不连续点是x=2和x=-2，故B正确．
C、若函数f（x）、g（x）满足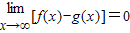
，则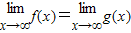
不一定成立，因为
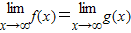成立的前提是
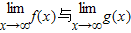必须都存在．故C不正确．
D、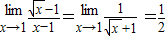
，故D正确．
故选C．
点评：本题考查极限的概念和函数的连续性，排除法是较好的解题方法．
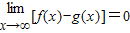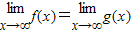，则不一定成立，因为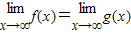成立的前提是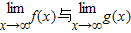必须都存在．故C不正确．解答：解：A、若函数f（x）在x=x处连续，则f（x）在x=x处有极限，所以
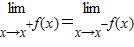，故A正确．B、函数
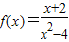的定义域是{x|x≠±2}，所以它的不连续点是x=2和x=-2，故B正确．C、若函数f（x）、g（x）满足
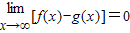，则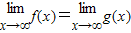不一定成立，因为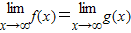成立的前提是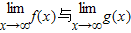必须都存在．故C不正确．D、
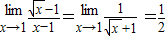，故D正确．故选C．
点评：本题考查极限的概念和函数的连续性，排除法是较好的解题方法．
练习册系列答案
相关题目