题目内容
已知函数f(x)=a+bsin2x+ccos2x的图象经过点A(0,1),B(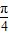 ,1),且当x∈[0,
,1),且当x∈[0,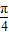 ]时,f(x)取得最大值2
]时,f(x)取得最大值2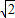 -1.
-1.(Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在向量m,使得将f(x)的图象按向量m平移后可以得到一个奇函数的图象?若存在,求出满足条件的一个m;若不存在,说明理由.
【答案】分析:(1)由已知中函数f(x)=a+bsin2x+ccos2x的图象经过点A(0,1),B(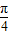 ,1),结合 当x∈[0,
,1),结合 当x∈[0,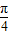 ]时,f(x)取得最大值2
]时,f(x)取得最大值2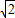 -1我们易求出a,b,c的值,进而求出f(x)的解析式;
-1我们易求出a,b,c的值,进而求出f(x)的解析式;
(Ⅱ)由已知中f(x)的解析式,根据正弦型函数的性质,可以求出他的图象的对称中心,将其对称中心平移到原点即可得到一个奇函数的图象,由此可得答案.
解答:解:(Ⅰ)由题意知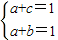 (2分)
(2分)
∴b=c=1-a,
∴f(x)=a+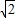 (1-a)sin(2x+
(1-a)sin(2x+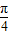 ).(1分)
).(1分)
∵x∈[0,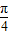 ],
],
∴2x+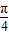 ∈[
∈[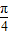 ,
,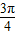 ].(1分)
].(1分)
当1-a>0时,
由a+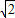 (1-a)=2
(1-a)=2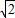 -1,
-1,
解得a=-1; (2分)
当1-a<0时,
a+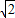 (1-a)•
(1-a)•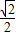 =2
=2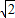 -1,无解; (1分)
-1,无解; (1分)
当1-a=0时,a=2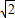 -1,相矛盾.(1分)
-1,相矛盾.(1分)
综上可知a=-1.(2分)
(Ⅱ)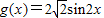 是奇函数,将g(x)的图象向左平移
是奇函数,将g(x)的图象向左平移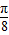 个单位,再向下平移一个单位就可以得到f(x)的图象.因此,将f(x)的图象向右平移
个单位,再向下平移一个单位就可以得到f(x)的图象.因此,将f(x)的图象向右平移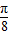 个单位,再向上平移一个单位就可以得到奇函数
个单位,再向上平移一个单位就可以得到奇函数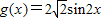 的图象.故
的图象.故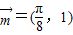 是满足条件的一个向量.(4分)
是满足条件的一个向量.(4分)
点评:本题考查的知识点是三角函数的最值,正弦函数的图象和性质,其中(1)中要注意对1-a>0时的符合进行分类讨论,尽管对答案无影响,但在题目答案的严谨性方面还是必要的.
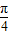 ,1),结合 当x∈[0,
,1),结合 当x∈[0,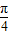 ]时,f(x)取得最大值2
]时,f(x)取得最大值2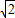 -1我们易求出a,b,c的值,进而求出f(x)的解析式;
-1我们易求出a,b,c的值,进而求出f(x)的解析式;(Ⅱ)由已知中f(x)的解析式,根据正弦型函数的性质,可以求出他的图象的对称中心,将其对称中心平移到原点即可得到一个奇函数的图象,由此可得答案.
解答:解:(Ⅰ)由题意知
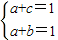 (2分)
(2分)∴b=c=1-a,
∴f(x)=a+
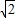 (1-a)sin(2x+
(1-a)sin(2x+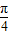 ).(1分)
).(1分)∵x∈[0,
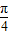 ],
],∴2x+
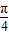 ∈[
∈[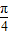 ,
,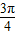 ].(1分)
].(1分)当1-a>0时,
由a+
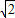 (1-a)=2
(1-a)=2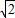 -1,
-1,解得a=-1; (2分)
当1-a<0时,
a+
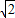 (1-a)•
(1-a)•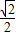 =2
=2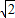 -1,无解; (1分)
-1,无解; (1分)当1-a=0时,a=2
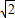 -1,相矛盾.(1分)
-1,相矛盾.(1分)综上可知a=-1.(2分)
(Ⅱ)
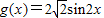 是奇函数,将g(x)的图象向左平移
是奇函数,将g(x)的图象向左平移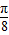 个单位,再向下平移一个单位就可以得到f(x)的图象.因此,将f(x)的图象向右平移
个单位,再向下平移一个单位就可以得到f(x)的图象.因此,将f(x)的图象向右平移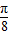 个单位,再向上平移一个单位就可以得到奇函数
个单位,再向上平移一个单位就可以得到奇函数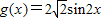 的图象.故
的图象.故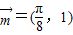 是满足条件的一个向量.(4分)
是满足条件的一个向量.(4分)点评:本题考查的知识点是三角函数的最值,正弦函数的图象和性质,其中(1)中要注意对1-a>0时的符合进行分类讨论,尽管对答案无影响,但在题目答案的严谨性方面还是必要的.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目