题目内容
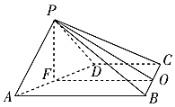
【题目】如图,在四棱锥P—ABCD中,四边形ABCD为平行四边形,BD⊥DC,△PCD为正三角形,平面PCD⊥平面ABCD,E为PC的中点.
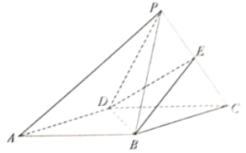
(1)证明:AP∥平面EBD;
(2)证明:BE⊥PC.
【答案】(1)见解析(2)见解析
【解析】
(1)连结AC交BD于点O,连结OE,利用三角形中位线可得AP∥OE,从而可证AP∥平面EBD;
(2)先证明BD⊥平面PCD,再证明PC⊥平面BDE,从而可证BE⊥PC.
证明:(1)连结AC交BD于点O,连结OE
因为四边形ABCD为平行四边形
∴O为AC中点,
又E为PC中点,
故AP∥OE,
又AP![]() 平面EBD,OE
平面EBD,OE![]() 平面EBD
平面EBD
所以AP∥平面EBD;
(2)∵△PCD为正三角形,E为PC中点
所以PC⊥DE
因为平面PCD⊥平面ABCD,
平面PCD![]() 平面ABCD=CD,
平面ABCD=CD,
又BD![]() 平面ABCD,BD⊥CD
平面ABCD,BD⊥CD
∴BD⊥平面PCD
又PC![]() 平面PCD,故PC⊥BD
平面PCD,故PC⊥BD
又BD![]() DE=D,BD
DE=D,BD![]() 平面BDE,DE
平面BDE,DE![]() 平面BDE
平面BDE
故PC⊥平面BDE
又BE![]() 平面BDE,
平面BDE,
所以BE⊥PC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: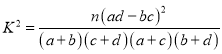 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
数学成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
物理成绩 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②根据上表数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
附:线性回归方程![]() ,
,
其中 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |