题目内容
(本小题满分12分,(Ⅰ)小问3分,(Ⅱ)小问5分,(Ⅲ)小问4分)
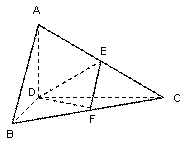
已知正△![]() 的边长为4,
的边长为4,![]() 是
是![]() 边上的高,
边上的高,![]() 分别是
分别是![]() 和
和![]() 边的中点,现将△
边的中点,现将△![]() 沿
沿![]() 翻折成直二面角
翻折成直二面角![]() ,如图所示.
,如图所示.
(I)证明:![]() ∥平面
∥平面![]() ;
;
(II)求二面角![]() 的余弦值;
的余弦值;
|
|
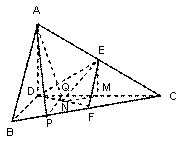
解:法一:(I)证明:如图:在△ABC中,由E、F分别是AC、BC中点,
得EF//AB,又AB![]() 平面DEF,EF
平面DEF,EF![]() 平面DEF.
平面DEF.
 ∴AB∥平面DEF. ……………………………………………………………………3分
∴AB∥平面DEF. ……………………………………………………………………3分
(II)∵AD⊥CD,BD⊥CD
∴∠ADB是二面角A—CD—B的平面角
∴AD⊥BD ∴AD⊥平面BCD
取CD的中点M,这时EM∥AD ∴EM⊥平面BCD
过M作MN⊥DF于点N,连结EN,则EN⊥DF
∴∠MNE是二面角E—DF—C的平面角, ………………………………………6分
在Rt△EMN中,EM=1,MN=![]()
∴tan∠MNE=![]() ,cos∠MNE=
,cos∠MNE=![]() . ………………………………………8分
. ………………………………………8分
(Ⅲ)在线段BC上存在点P,使AP⊥DE ………………………………………9分
证明:在线段BC上取点P,使![]() ,过P作PQ⊥CD与点Q,
,过P作PQ⊥CD与点Q,
∴PQ⊥平面ACD ∵![]() 在等边△ADE中,∠DAQ=30°
在等边△ADE中,∠DAQ=30°
∴AQ⊥DE∴AP⊥DE. …………………………………………12分
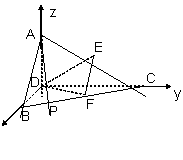 法二:(Ⅱ)以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,则A(0,0,2)B(2,0,0)C(0,
法二:(Ⅱ)以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,则A(0,0,2)B(2,0,0)C(0,![]() ,平面CDF的法向量为
,平面CDF的法向量为![]() 设平面EDF的法向量为
设平面EDF的法向量为![]()
则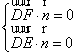 即
即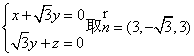
|
所以二面角E—DF—C的余弦值为![]() . ……………………………………8分
. ……………………………………8分
(Ⅲ)在平面坐标系xDy中,直线BC的方程为![]()
设![]()
![]()
所以在线段BC上存在点P,使AP⊥DE. ……………………………………12分

 口算能手系列答案
口算能手系列答案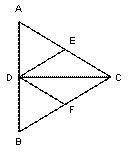 第20题图
第20题图