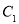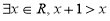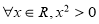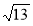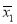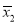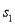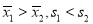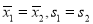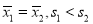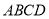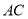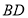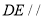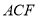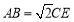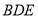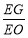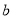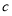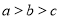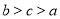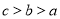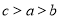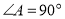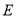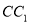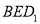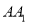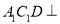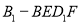题目内容
在一个花瓶中装有6枝鲜花,其中3枝山茶花,2枝杜鹃花和1枝君子兰,从中任取2枝鲜花.
(1)求恰有一枝山茶花的概率;
(2)求没有君子兰的概率.
(1)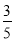 ;(2)
;(2) .
.
【解析】
试题分析:本题是古典概型的概率计算问题,古典概型的概率计算,关键是计算出基本事件总数,某个事件发生时所包含的基本事件数,然后代入公式即可求解,本题采用列举法找出从6枝鲜花中任取2枝鲜花的所有可能有15种,对于(1)“恰有一枝山茶花”事件包含了9种基本事件,对于(2)“没有君子兰”事件则包含了10种基本事件,然后按照古典概率的计算公式进行计算即可.
试题解析:设3枝山茶花为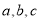 ,2枝杜鹃花为
,2枝杜鹃花为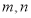 ,1枝君子兰为
,1枝君子兰为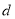 . 则从6枝鲜花中任取2枝的基本事件有:
. 则从6枝鲜花中任取2枝的基本事件有: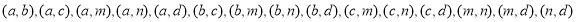 , 共15种 4分
, 共15种 4分
(1)其中恰有一枝山茶花的基本事件有: 共9种,所以恰有一枝山茶花的概率为
共9种,所以恰有一枝山茶花的概率为 8分
8分
(2)其中没有君子兰的基本事件有: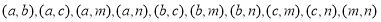 共10种,所以没有君子兰的概率为
共10种,所以没有君子兰的概率为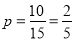 12分.
12分.
考点:古典概型的概率计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在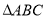 中,
中,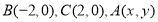 ,给出
,给出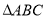 满足的条件,就能得到动点
满足的条件,就能得到动点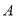 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
条件 | 方程 |
① |
|
② |
|
③ |
|
则满足条件①、②、③的点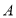 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A. 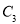 、
、 、
、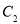 B.
B. 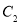 、
、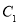 、
、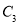
C. 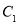 、
、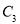 、
、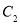 D.
D. 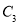 、
、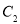 、
、