题目内容
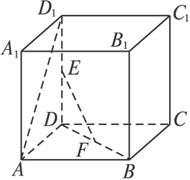
 如图,正方体AC1中,
如图,正方体AC1中,| DF |
| DD1 |
| AE |
| AA1 |
| 2 |
| 3 |
| CG |
| CC1 |
| BH |
| BB1 |
| 1 |
| 3 |
| A、抛物线 | B、圆 | C、椭圆 | D、双曲线 |
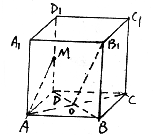
分析:如图所示.不妨是正方体的棱长为1.由题意可知:对角线AC1与平面EFGH的交点为AC1的中点.由已知满足∠PAA1=∠C1AA1,可知:tan∠PAA1=tan∠C1AA1=
=
.作正方体AC1的平行于底面ABCD的中截面(线段AA1的中点是O),可得:中截面内满足tan∠QAA1=
的点Q的轨迹是圆弧MPN,满足OQ=OM=ON=OP=
.则AQ或延长AQ与平面EFGH的交点即为点P的轨迹,其轨迹是椭圆的一部分.
| A1C1 |
| AA1 |
| 2 |
| 2 |
| ||
| 2 |
解答:解:如图所示.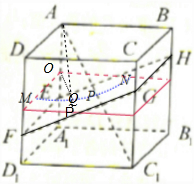 不妨是正方体的棱长为1.
不妨是正方体的棱长为1.
由题意可知:对角线AC1与平面EFGH的交点为AC1的中点.
由满足∠PAA1=∠C1AA1,则tan∠PAA1=tan∠C1AA1=
=
.
作正方体AC1的平行于底面ABCD的中截面(线段AA1的中点是O),在中截面内满足tan∠QAA1=
的点Q的轨迹是圆弧MPN,
满足OQ=OM=ON=OP=
.
则AQ或延长AQ与平面EFGH的交点即为点P的轨迹,其轨迹是椭圆的一部分.
故选:C.
 不妨是正方体的棱长为1.
不妨是正方体的棱长为1.由题意可知:对角线AC1与平面EFGH的交点为AC1的中点.
由满足∠PAA1=∠C1AA1,则tan∠PAA1=tan∠C1AA1=
| A1C1 |
| AA1 |
| 2 |
作正方体AC1的平行于底面ABCD的中截面(线段AA1的中点是O),在中截面内满足tan∠QAA1=
| 2 |
满足OQ=OM=ON=OP=
| ||
| 2 |
则AQ或延长AQ与平面EFGH的交点即为点P的轨迹,其轨迹是椭圆的一部分.
故选:C.
点评:本题考查了圆的定义、椭圆的定义、角相等的应用,属于难题.

练习册系列答案
相关题目
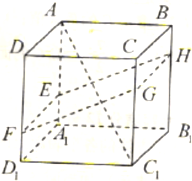
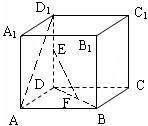 如图,正方体AC1中,E、F分别是DD1、BD的中点,则直线AD1与EF所成的角余弦值是( ).
如图,正方体AC1中,E、F分别是DD1、BD的中点,则直线AD1与EF所成的角余弦值是( ).A、
| ||||
B、
| ||||
C、
| ||||
D、
|
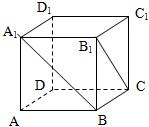 3、如图,正方体AC1中,直线A1B与B1C所成的角的大小是( )
3、如图,正方体AC1中,直线A1B与B1C所成的角的大小是( )