题目内容
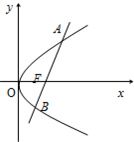 已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.
已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.(1)若|AF|=4,求点A的坐标;
(2)若直线l的倾斜角为45°,求线段AB的长.
分析:(1)由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).设A(x1,y1),B(x2,y2).由抛物线的定义可知,|AF|=x1+
,从而x1=3.由此能得到点A的坐标.
(2)直线l的方程为y=x-1.与抛物线方程联立,得
,整理得x2-6x+1=0,其两根为x1,x2,且x1+x2=6.由抛物线的定义可知线段AB的长.
| p |
| 2 |
(2)直线l的方程为y=x-1.与抛物线方程联立,得
|
解答: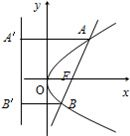 解:由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).(2分)
解:由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).(2分)
设A(x1,y1),B(x2,y2).
(1)由抛物线的定义可知,|AF|=x1+
,从而x1=3.
代入y2=4x,解得y1=±2
.
∴点A的坐标为(3,2
)或(3,-2
).(6分)
(2)直线l的方程为y-0=tan45°(x-1),即y=x-1.
与抛物线方程联立,得
,(9分)
消y,整理得x2-6x+1=0,其两根为x1,x2,且x1+x2=6.
由抛物线的定义可知,|AB|=p+x1+x2=6+2=8.
所以,线段AB的长是8.(12分)
 解:由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).(2分)
解:由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).(2分)设A(x1,y1),B(x2,y2).
(1)由抛物线的定义可知,|AF|=x1+
| p |
| 2 |
代入y2=4x,解得y1=±2
| 3 |
∴点A的坐标为(3,2
| 3 |
| 3 |
(2)直线l的方程为y-0=tan45°(x-1),即y=x-1.
与抛物线方程联立,得
|
消y,整理得x2-6x+1=0,其两根为x1,x2,且x1+x2=6.
由抛物线的定义可知,|AB|=p+x1+x2=6+2=8.
所以,线段AB的长是8.(12分)
点评:本题考查直线和抛物线的位置关系,解题时要认真审题,合理地进行等价转化,注意抛物线性质的合理运用.

练习册系列答案
相关题目
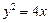 的焦点F,
的焦点F,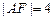 ,求点A的坐标;
,求点A的坐标;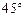 ,求线段AB的长.
,求线段AB的长.
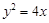 的焦点F,
的焦点F,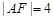 ,求点A的坐标;
,求点A的坐标;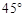 ,求线段AB的长.
,求线段AB的长.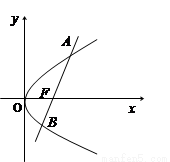
 的焦点F,且与抛物线相交于A、B两点.
的焦点F,且与抛物线相交于A、B两点.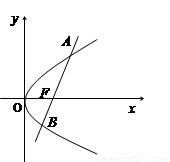
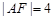 ,求点A的坐标;
,求点A的坐标;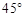 ,求线段AB的长.
,求线段AB的长.