题目内容

18．已知函数f（x）=x+$\frac{4}{x}$，x∈（0，2]，那么函数有没有最大值、最小值？若有，请求出；若没有，请说明原因．

分析 求出函数的导数，求得f（x）在（0，2]的单调性，即可得到最值．

解答 解：函数f（x）=x+$\frac{4}{x}$的导数为
f′（x）=1-$\frac{4}{{x}^{2}}$，
f（x）在（0，2]上f′（x）＜0，f（x）递减，
则x=2时，取得最小值4．
无最大值．

点评 本题考查函数的最值的求法，考查函数的单调性的应用，属于基础题．

练习册系列答案
相关题目
8．设i是虚数单位，则复数$\frac{1-3i}{i^3}$等于（　　）
A．-3+iB．-3-iC．3+iD．3-i
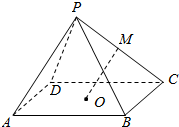9．如图，在四棱锥P-ABCD中，底面是正方形，中心为O，且底面边长和侧棱长相等，M是PC的中点，求MO与AB所成的角．
6．在下列平面直角坐标系中，分别作出椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1；
（1）x轴与y轴具有同的单位长度；
（2）x轴上的单位长度为y轴上单位长度的2倍；
（3）x轴上的单位长度为y轴上单位长度的$\frac{1}{2}$倍．
13．利用定义判断f（x）=$\frac{2x}{x+3}$在区间（0，+∞）上的单调性．
3．若平面α的斜线l在α上的射影为l′，直线b∥α且b⊥l′，则b与l（　　）
A．必相交B．必为异面直线C．垂直D．无法确定
10．作出下列函数的图象．
（1）y=2x，x∈{-2，-1，0，1，2}；
（2）y=2x-1，x∈{x|-1＜x＜1}；
（3）y=|x|，x∈R；
（4）y=$\frac{2}{x}$，x∈{x|1＜x＜4}；
（5）y=|x-5|+2，x∈R．
7．已知函数f（x）=$\frac{2x+4}{x+1}$．
（1）求f（x）的定义域，对称中心及单调区间；
（2）令g（x）=f（x）+x，证明：g（x）在（$\sqrt{2}$-1，+∞）上单调递增；
（3）不等式|f（x）|＜2a+1恰有两个整数解，求a的取值范围．
8．（1）已知f（x+$\frac{1}{x}$）=x3+$\frac{1}{{x}^{3}}$，求f（x）的表达式；
（2）给出函数y=x+$\frac{a}{x}$（a＞0）的单调性；在（-∞，-$\sqrt{a}$]，[$\sqrt{a}$，+∞）上单调递增，在[（-$\sqrt{a}$，0），（0，$\sqrt{a}$）]上单调递减，利用这一结论，求第（2）问中所得f（x）的定义域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网