题目内容
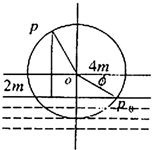 如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.
如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
(2)点p第一次到达最高点大约需要多少时间?
分析:(1)先根据z的最大和最小值求得A和B,利用周期求得ω,当x=0时,z=0,进而求得φ的值,则函数的表达式可得;
(2)令最大值为6,即 z=4sin(
t-
)+2=6可求得时间.
(2)令最大值为6,即 z=4sin(
| π |
| 6 |
| π |
| 6 |
解答:解:(1)依题意可知z的最大值为6,最小为-2,
∴
⇒
;
∵op每秒钟内所转过的角为(
)=
t,得z=4sin(
t+φ)+2,
当t=0时,z=0,得sinφ=-
,即φ=-
,故所求的函数关系式为
z=4sin(
t-
)+2
(2)令z=4sin(
t-
)+2=6,得sin(
t-
)=1,
取
t-
=
,得t=4,
故点P第一次到达最高点大约需要4S.
∴
|
|
∵op每秒钟内所转过的角为(
| 5×2π |
| 60 |
| π |
| 6 |
| π |
| 6 |
当t=0时,z=0,得sinφ=-
| 1 |
| 2 |
| π |
| 6 |
z=4sin(
| π |
| 6 |
| π |
| 6 |
(2)令z=4sin(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
取
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
故点P第一次到达最高点大约需要4S.
点评:本题主要考查了在实际问题中建立三角函数模型的问题.考查了运用三角函数的最值,周期等问题确定函数的解析式.

练习册系列答案
相关题目
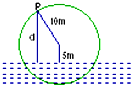 如图,一个半径为10米的水轮按逆时针方向每分钟转4圈,记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),
如图,一个半径为10米的水轮按逆时针方向每分钟转4圈,记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:d=Asin(ωt+φ)+k(A>0,ω>0),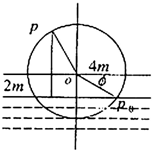 如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.
如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.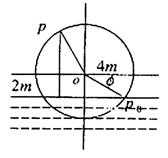
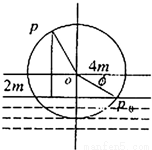 如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p)开始计算时间.
如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p)开始计算时间.