题目内容
(选修4-2:矩阵与变换)已知矩阵A=
 ,若矩阵A属于特征值6的一个特征向量为α1=
,若矩阵A属于特征值6的一个特征向量为α1= ,属于特征值1的一个特征向量为α2=
,属于特征值1的一个特征向量为α2= .
.①求矩阵A;②求直线y=x+2在矩阵A的作用下得到的曲线方程.
【答案】分析:①根据特征值的定义可知Aα=λα,利用待定系数法建立四个等式关系,解二元一次方程组即可.
②设直线y=x+2上任意一点(x,y),(x',y')是所得的直线上一点,根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标用未知的坐标表示,代入已知直线的方程,得到结果.
解答:解:①由矩阵A属于特征值6的一个特征向量为 可得
可得 
 =6
=6  ,
,
即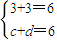 ;
;
由矩阵A属于特征值1的一个特征向量为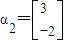 ,可得
,可得 
 =
= ,
,
即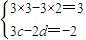
解得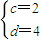 ,即矩阵
,即矩阵 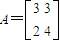 .
.
②设y=x+2上一点(x,y)在A作用下变为(x′,y′),
则
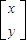 =
= ,
,
∴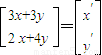 ,
,
∴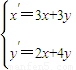 ,∴
,∴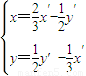 ,
,
∵y=x+2,代入得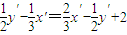 ,
,
化简,得y′=x′+2,
∴变换后的直线方程是:y=x+2.
点评:本题主要考查了二阶矩阵,以及特征值与特征向量的计算,考查矩阵的变换,属于基础题.
②设直线y=x+2上任意一点(x,y),(x',y')是所得的直线上一点,根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标用未知的坐标表示,代入已知直线的方程,得到结果.
解答:解:①由矩阵A属于特征值6的一个特征向量为
 可得
可得 
 =6
=6  ,
,即
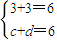 ;
;由矩阵A属于特征值1的一个特征向量为
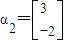 ,可得
,可得 
 =
= ,
,即
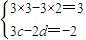
解得
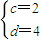 ,即矩阵
,即矩阵 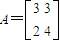 .
.②设y=x+2上一点(x,y)在A作用下变为(x′,y′),
则

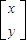 =
= ,
,∴
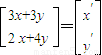 ,
,∴
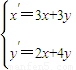 ,∴
,∴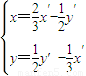 ,
,∵y=x+2,代入得
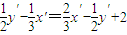 ,
,化简,得y′=x′+2,
∴变换后的直线方程是:y=x+2.
点评:本题主要考查了二阶矩阵,以及特征值与特征向量的计算,考查矩阵的变换,属于基础题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 (2012•江苏一模)选做题
(2012•江苏一模)选做题