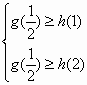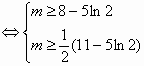Question

已知函数，g(x)＝f(x)＋ax－6lnx，其中a∈R．

(Ⅰ)当a＝1时判断f(x)的单调性；

(Ⅱ)若g(x)在其定义域内为增函数，求正实数a的取值范围；

(Ⅲ)设函数h(x)＝x²－mx＋4，当a＝2时，若，，总有成立，求实数m的取值范围．

Answer 1

答案：
解析：

解：(Ⅰ)的定义域为， 　　且＞0 　　所以f(x)为增函数　　3分 　　(Ⅱ)，的定义域为 　　 　　因为在其定义域内为增函数，所以， 　　 　　而，当且仅当时取等号， 　　所以　　8分 　　(Ⅲ)当时，， 　　由得或 　　当时，；当时，． 　　所以在上， 　　而“，，总有成立”等价于 　　“在上的最大值不小于在上的最大值” 　　而在上的最大值为 　　所以有 　　 　　所以实数的取值范围是　　13分