题目内容
“ ”是“函数
”是“函数 在区间
在区间 上存在零点
上存在零点 ”的
”的
 ”是“函数
”是“函数 在区间
在区间 上存在零点
上存在零点 ”的
”的| A.充分非必要条件 | B.必要非充分条件 |
| C.充分必要条件 | D.既非充分也非必要条件 |
A
专题:综合题.
分析:我们可以根据充分、充要条件的定义进行判断.
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
解答:∵a<-2,f(x)=ax+3,
∴f(0)=3>0,f(2)=2a+3<2×(-2)+3=-1<0,f(0)?f(2)<0
∴函数f(x)=ax+3在区间[-1,2]上存在零点x0.
∴a<-2”是“函数f(x)=ax+3在区间[-1,2]上存在零点x0”的充分条件;
反之,若函数f(x)=ax+3在区间[-1,2]上存在零点,则f(-1)?f(2)≤0,即(-a+3)(2a+3)≤0解得a≤-
 或a≥3,
或a≥3,∴a<-2不是“函数f(x)=ax+3在区间[-1,2]上存在零点的必要条件.
故选A.
点评:本题考查充分、充要条件的判断方法,我们可以根据充分、充要条件的定义进行判断,解题的关键是零点存在性定理的正确使用.

练习册系列答案
相关题目
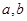 和平面
和平面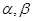 ,
,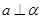 ,
,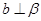 ,则“
,则“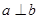 ”是“
”是“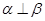 ”的( )
”的( )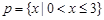 ,
,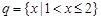 ,那么“
,那么“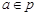 ”是“
”是“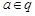 ”的
”的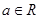 ,则
,则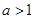 是
是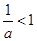 的 ( )
的 ( ) 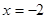 ”是“
”是“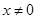 ”的
”的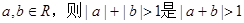 的充分不必要条件;
的充分不必要条件;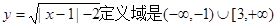 ,则 ( )
,则 ( ) ”为真
”为真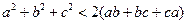 ”的 ( )
”的 ( ) 条件 B.必要非充分条件
条件 B.必要非充分条件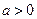 ”是“
”是“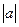 >0”的 ( )
>0”的 ( )