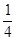题目内容
已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使得g(x)=f(x)-x|x|在R上是奇函数或是偶函数?若存在,求出a的值,若不存在,请说明理由.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使得g(x)=f(x)-x|x|在R上是奇函数或是偶函数?若存在,求出a的值,若不存在,请说明理由.
(1)当a=-1时,f(x)=x2+(x-1)|x+1|,
故有,f(x)=
,
当x≥-1时,由f(x)=1,有2x2-1=1,解得x=1,或x=-1.
当x<-1时,f(x)=1恒成立,
∴方程的解集为{x|x≤-1或x=1}.
(2)f(x)=
,
若f(x)在R上单调递增,
则有
,解得,a≥
.
∴当a≥
时,f(x)在R上单调递增.
(3)g(x)=x2+(x-1)|x+a|-x|x|,
∵g(1)=0,g(-1)=2-2|a-1|,
若存在实数a,使得g(x)在R上是奇函数或是偶函数,
则必有g(-1)=0,
∴2-2|a-1|=0,∴a=0,或a=2.
①若a=0,则g(x)=x2+(x-1)|x|-x|x|=x2-|x|,
∴g(-x)=g(x)对x∈R恒成立,∴g(x)为偶函数.
②若a=2,则g(x)=x2+(x-1)|x+2|-x|x|,
∴g(2)=4,g(-2)=8,∴g(-2)≠g(2)且g(-2)≠-g(2),
∴g(x)为非奇非偶函数,
∴当a=0时,g(x)为偶函数;当a≠0时,g(x)为非奇非偶函数.
故有,f(x)=
|
当x≥-1时,由f(x)=1,有2x2-1=1,解得x=1,或x=-1.
当x<-1时,f(x)=1恒成立,
∴方程的解集为{x|x≤-1或x=1}.
(2)f(x)=
|
若f(x)在R上单调递增,
则有
|
| 1 |
| 3 |
∴当a≥
| 1 |
| 3 |
(3)g(x)=x2+(x-1)|x+a|-x|x|,
∵g(1)=0,g(-1)=2-2|a-1|,
若存在实数a,使得g(x)在R上是奇函数或是偶函数,
则必有g(-1)=0,
∴2-2|a-1|=0,∴a=0,或a=2.
①若a=0,则g(x)=x2+(x-1)|x|-x|x|=x2-|x|,
∴g(-x)=g(x)对x∈R恒成立,∴g(x)为偶函数.
②若a=2,则g(x)=x2+(x-1)|x+2|-x|x|,
∴g(2)=4,g(-2)=8,∴g(-2)≠g(2)且g(-2)≠-g(2),
∴g(x)为非奇非偶函数,
∴当a=0时,g(x)为偶函数;当a≠0时,g(x)为非奇非偶函数.

练习册系列答案
相关题目
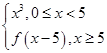 ,那么f(2 013)=________.
,那么f(2 013)=________.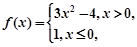 ,则
,则 .
. ,若
,若 ,则a=
,则a=