题目内容

已知函数f(x)=
x2
x2+1
，则f(1)+f(2)+…+f(2013)+f(2014)+f(
1
2
)+f(
1
3
)+…+f(
1
2013
)+f(
1
2014
)=（　　）
A．2010
1
2
B．2011
1
2
C．2012
1
2
D．2013
1
2
∵已知函数f(x)=
x2
x2+1
，
∴f（
1
x
）=
1
x2
1
x2
+1
=
1
1+x2
，
∴f（x）+f（
1
x
）=1．
则f(1)+f(2)+…+f(2013)+f(2014)+f(
1
2
)+f(
1
3
)+…+f(
1
2013
)+f(
1
2014
)
=f（1）+[f（2）+f（
1
2
）]+[f（3）+f（
1
3
）+…+[f（2014）+f（
1
2014
）]
=
1
2
+1+1+…+1=
1
2
+2013×1=2013
1
2
，
故选：D．
练习册系列答案
相关题目
已知函数f（x）是偶函数，且它在[0，+∞）上是减函数，若f（lgx）＞f（1），则x的取值围是______．
已知函数f(x)=a-
1
|2x-b|
是偶函数，a为实常数．
（1）求b的值；
（2）当a=1时，是否存在m，n（n＞m＞0）使得函数y=f（x）在区间[m，n]上的函数值组成的集合也是[m，n]，若存在，求出m，n的值，否则，说明理由；
（3）若在函数定义域内总存在区间[m，n]（m＜n），使得y=f（x）在区间[m，n]上的函数值组成的集合也是[m，n]，求实数a的取值范围．
定义在区间[-
2
3
π，π]上的函数y=f（x）的图象关于直线x=
π
6
对称，当x∈[-
2
3
π，
π
6
]时，函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其图象如图所示．

（Ⅰ）求函数y=f（x）在[-
2
3
π，π]的表达式；
（Ⅱ）求方程f（x）=
2
的解；
（Ⅲ）是否存在常数m的值，使得|f（x）-m|＜2在x∈[-
2π
3
，π]上恒成立；若存在，求出m的取值范围；若不存在，请说明理由．
已知函数f（x）=x2+（x-1）|x-a|．
（1）若a=-1，解方程f（x）=1；
（2）若函数f（x）在R上单调递增，求实数a的取值范围；
（3）是否存在实数a，使得g（x）=f（x）-x|x|在R上是奇函数或是偶函数？若存在，求出a的值，若不存在，请说明理由．
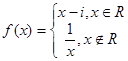已知定义在复数集C上的函数，则在复平面内对应的点位于第______象限．
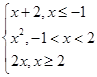已知函数f(x)＝，若f(x)＝3，则x的值是        ．
已知实数，函数，若，则的值为     ．
若，则_________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网