题目内容
设函数f(x)=x4+ax3+2x2+b(x∈R),其中a,b∈R.
(Ⅰ)当![]() 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)仅在x=0处有极值,求a的取值范围;
(Ⅲ)若对于任意的a∈[-2,2],不等式f(x)≤1在[-1,1]上恒成立,求b的取值范围.
答案:
解析:
解析:
|
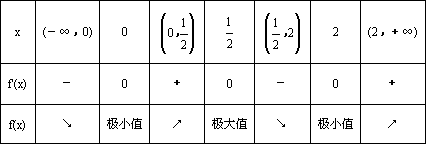
(Ⅰ)解: 当 令 当
所以 (Ⅱ)解: 为使 解此不等式,得 因此满足条件的 (Ⅲ)解:由条件 当 因此函数 为使对任意的 在 所以 本小题主要考查利用导数研究函数的单调性和极值、函数的最大值、解不等式等基础知识,考查综合分析和解决问题的能力.满分14分. |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目