题目内容
设函数f(x)＝x4＋ax3＋2x2＋b(x∈R)，其中a，b∈R．
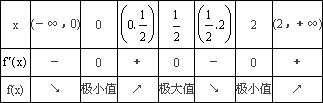
(Ⅰ)当a＝－
时，讨论函数f(x)的单调性；
(Ⅱ)若函数f(x)仅在x＝0处有极值，求a的取值范围；
(Ⅲ)若对于任意的a∈[－2，2]，不等式f(x)≤1在[－1，1]上恒成立，求b的取值范围．
答案：
解析：
解析：
|
所以f(x)在 (Ⅱ)解： 为使f(x)仅在x＝0处有极值，必须4x2＋3ax＋4≥0恒成立，即有Δ＝9a2－64≤0 8分 解此不等式，得 因此满足条件的a的取值范围是 (Ⅲ)解：由条件a∈[－2，2]可知Δ＝9a2－64＜0，从而4x2＋3ax＋4＞0恒成立． 当x＜0时， 因此函数f(x)在[－1，1]上的最大值是f(1)与f(－1)两者中的较大者 12分 为使对任意的a∈[－2，2]，不等式f(x)≤1在[－1，1]上恒成立，当且仅当 所以b≤－4，因此满足条件的b的取值范围是(－∞，－4] 14分 |
内是减函数 5分
，显然x＝0不是方程4x2＋3ax＋4＝0的根．
．这时，f(0)＝b是唯一极值．
10分
．
练习册系列答案
相关题目
时，讨论函数f(x)的单调性；
x2＋ax＋2lnx，a∈R，已知函数f(x)在x＝1
，e](其中e是自然对数的底数)时，证明：e(e－x)(e＋x－6)＋4≥x4
＜
n3－
n2＋
n