题目内容
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4.E是PD的中点.
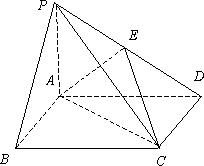
(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)求二面角E-AC-D所成平面角的余弦值;
(Ⅲ)求B点到平面EAC的距离.
解析:
解法一:
(Ⅰ)![]()
![]()
![]() 2分
2分
![]()
![]()
而![]()
![]() 4分
4分![]()
![]() 5分
5分
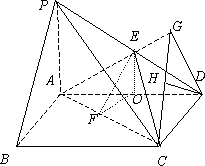
(Ⅱ)连结![]() 、
、![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,
则![]() 就是二面角
就是二面角![]() 所成平面角. 7分
所成平面角. 7分
由![]() ,则
,则![]() .
.
在![]() 中,
中,![]() 解得
解得![]()
![]()
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() 8分
8分
而![]() ,由勾股定理可得
,由勾股定理可得![]() 9分
9分
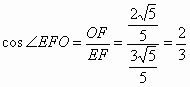 10分
10分
(Ⅲ)连结![]() ,在三棱锥
,在三棱锥![]() 中,
中,![]()
![]() 12分
12分
点![]() 到底面
到底面![]() 的距离
的距离![]() ,
,
则由![]() ,即
,即![]() 13分
13分
![]() 求得
求得![]()
所以![]() 点到平面
点到平面![]() 的距离是
的距离是![]() . 14分
. 14分
解法二:
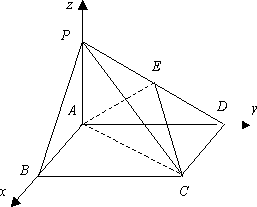
以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() (0,0,0),
(0,0,0),![]() (2,0,0),
(2,0,0),![]() (2,4,0),
(2,4,0),![]() (0,4,0),
(0,4,0),
![]() (0,2,1),
(0,2,1),![]() (0,0,2). 2分
(0,0,2). 2分
∴![]() =(2,0,0),
=(2,0,0),![]() =(0,4,0),
=(0,4,0),![]() =(0,0,2),
=(0,0,2),![]() =(-2,0,0),
=(-2,0,0),
![]() =(0,2,1),
=(0,2,1),![]() =(2,4,0), 3分
=(2,4,0), 3分
(Ⅰ)![]()
![]()
又![]()
![]() 5分
5分
![]()
![]() 而
而![]()
∴平面![]() ⊥平面
⊥平面![]() . 7分
. 7分
(Ⅱ)设平面![]() 的法向量
的法向量![]()
由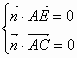 即
即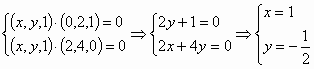
∴![]() =
=![]() . 9分
. 9分
平面![]() 的法向量
的法向量![]() =(0,0,2),
=(0,0,2),
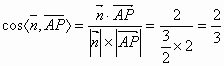
所以二面角![]() 所成平面角的余弦值是
所成平面角的余弦值是![]() . 11分
. 11分
(Ⅲ)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
![]() =(2,0,0),
=(2,0,0),![]() =
=![]() . 12分
. 12分
则![]() =
=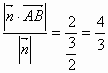
所以![]() 点到平面
点到平面![]() 的距离是
的距离是![]() . 14分
. 14分

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 (2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.
(2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点. 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4. (2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证:
(2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证: 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.