题目内容
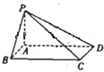 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)在BC边上是否存在一点M,使得D点到平面PAM的距离为2,若存在,求BM的值,若不存在,请说明理由.
分析:(Ⅰ)要证平面PDC⊥平面PAD,只要证明DC⊥平面PAD即可,由PA⊥底面ABCD,底面ABCD为矩形可以得到证明;
(Ⅱ)假设存在,设出BM的长度,利用等积法求出BM,只要BM的长度不超过4说明假设成立,否则假设不成立.
(Ⅱ)假设存在,设出BM的长度,利用等积法求出BM,只要BM的长度不超过4说明假设成立,否则假设不成立.
解答: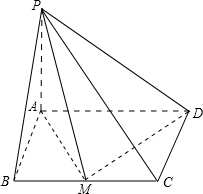 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,
∵ABCD是矩形,∴CD⊥AB,
又∵PA⊥底面ABCD,且CD?平面ABCD,
∴CD⊥PA.
又∵PA∩AD=A,
∴CD⊥平面PAD,
又∵CD?平面PDC,
∴平面PDC⊥平面PAD;
(Ⅱ)解:假设BC边上存在一点M满足题设条件,令BM=x,
∵AB=2,BC=4.且PA⊥底面ABCD,PA=2,
则在Rt△ABM中,AM=
=
,
∵PA⊥底面ABCD,
∴SRt△PAM=
PA•AM=
,
S△AMD=
AD•AB=4.
又∵VP-AMD=VD-PAM,
∴
×2×4=
×2×
,解得x=2
<4.
故存在点M,当BM=2
时,使点D到平面PAM的距离为2.
 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,∵ABCD是矩形,∴CD⊥AB,
又∵PA⊥底面ABCD,且CD?平面ABCD,
∴CD⊥PA.
又∵PA∩AD=A,
∴CD⊥平面PAD,
又∵CD?平面PDC,
∴平面PDC⊥平面PAD;
(Ⅱ)解:假设BC边上存在一点M满足题设条件,令BM=x,
∵AB=2,BC=4.且PA⊥底面ABCD,PA=2,
则在Rt△ABM中,AM=
| AB2+BM2 |
| 4+x2 |
∵PA⊥底面ABCD,
∴SRt△PAM=
| 1 |
| 2 |
| 4+x2 |
S△AMD=
| 1 |
| 2 |
又∵VP-AMD=VD-PAM,
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 4+x2 |
| 3 |
故存在点M,当BM=2
| 3 |
点评:本题考查了平面与平面垂直的判定,考查了空间距离的求法,训练了“等积法”求点到面的距离,是中档题.

练习册系列答案
相关题目
 (2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.
(2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.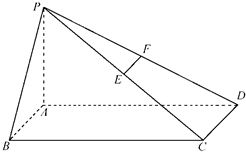 (2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证:
(2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证: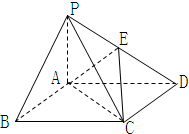 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点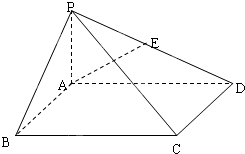 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.