题目内容
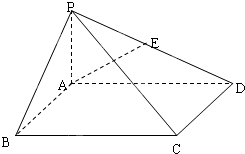 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=1,BC=2.(1)若E为PD的中点,求异面直线AE与PC所成角的余弦值;
(2)在BC上是否存在一点G,使得D到平面PAG的距离为1?若存在,求出BG;若不存在,请说明理由.
分析:以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,推出A,B,C,D,E,P坐标
(1)利用cos<
>=
,求异面直线AE与PC所成角的余弦值.
(2)假设存在,设BG=x,则G(1,x,0),作DQ⊥AG,利用2S△ADG=SABCD,求出x值,说明存在点G满足题意.
(1)利用cos<
| AE, |
| PC |
| ||||
|
|
(2)假设存在,设BG=x,则G(1,x,0),作DQ⊥AG,利用2S△ADG=SABCD,求出x值,说明存在点G满足题意.
解答: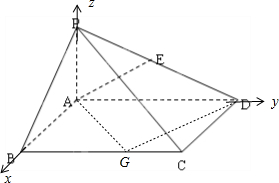 解:以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,
解:以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,
建立空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),
E(0,1,
),P(0,0,1),
=(-1,0,0),
=(0,2,0),
=(0,0,1),
=(0,1,
),
=(1,2,-1)
(1)∵cos<
>=
=
,
所求异面直线AE与PC所成角的余弦值为
…(6分)
(2)假设存在,设BG=x,则G(1,x,0),
作DQ⊥AG,则DQ⊥平面PAG,即DG=1,
∵2S△ADG=SABCD,
∴|
||
|=|
||
|,∴AG=
=2⇒x=
,
故存在点G,当BG=
时,D到平面PAG的距离为1.….(12分)
 解:以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,
解:以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),
E(0,1,
| 1 |
| 2 |
| CD |
| AD |
| AP |
| AE |
| 1 |
| 2 |
| PC |
(1)∵cos<
| AE, |
| PC |
| ||||
|
|
| ||
| 10 |
所求异面直线AE与PC所成角的余弦值为
| ||
| 10 |
(2)假设存在,设BG=x,则G(1,x,0),
作DQ⊥AG,则DQ⊥平面PAG,即DG=1,
∵2S△ADG=SABCD,
∴|
| AG |
| DQ |
| AB |
| AD |
| 1+x2 |
| 3 |
故存在点G,当BG=
| 3 |
点评:本题考查用空间向量求直线间的夹角、距离,点、线、面间的距离计算,考查空间想象能力,计算能力.

练习册系列答案
相关题目
 (2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.
(2012•惠州模拟)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=2,E是PD的中点.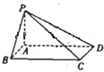 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=2,BC=4.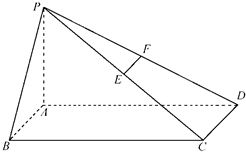 (2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证:
(2010•通州区一模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,E、F分别是PC、PD的中点,求证: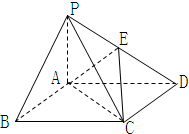 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点