题目内容
在△ 中,已知
中,已知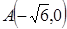 、
、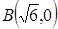 ,动点
,动点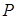 满足
满足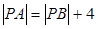 .
.
(1)求动点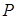 的轨迹方程;
的轨迹方程;
(2)设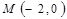 ,
,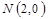 ,过点
,过点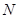 作直线垂直于
作直线垂直于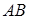 ,且与直线
,且与直线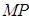 交于点
交于点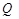 ,试在
,试在 轴上确定一点
轴上确定一点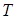 ,使得
,使得 ;
;
(3)在(II)的条件下,设点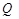 关于
关于 轴的对称点为
轴的对称点为 ,求
,求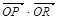 的值.
的值.
【答案】
(1)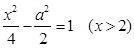 ;(2)
;(2)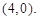 ;(3)
;(3)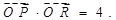 .
.
【解析】本试题主要考查了双曲线的定义求解轨迹方程的运用,以及直线与双曲线的位置关系 综合运用。
解:(1) ,∴ 动点
,∴ 动点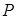 的轨迹是以
的轨迹是以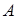 、
、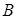 为焦点的双曲线的右支除去其与x轴的交点. 设双曲线方程为
为焦点的双曲线的右支除去其与x轴的交点. 设双曲线方程为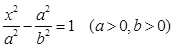 .
.
由已知,得 解得
解得
∴ .
.
∴动点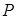 的轨迹方程为
的轨迹方程为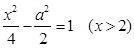 .
.
注:未去处点(2,0),扣1分
(2)由题意,直线 的斜率存在且不为0,设直线l的方程x =2.
的斜率存在且不为0,设直线l的方程x =2.
设 的方程为
的方程为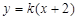 .
.
∵点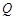 是与直线
是与直线 的交点,∴
的交点,∴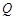
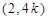 .设
.设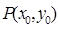
由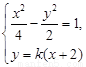 整理得
整理得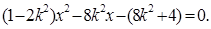
则此方程必有两个不等实根
 ,且
,且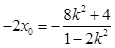 .
.
∴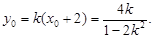 ∴
∴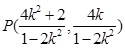 .
.
设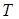
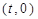 ,要使得
,要使得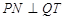 ,只需
,只需
由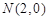 ,
,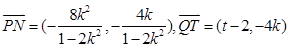 ,
,
∴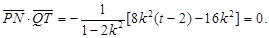
∵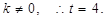 此时
此时 ∴所求
∴所求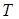 的坐标为
的坐标为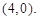
(3)由(II)知
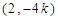 ,∴
,∴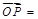
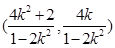 ,
,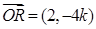 .
.
∴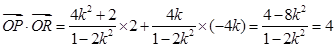 .
.
∴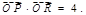
说明 其他正确解法按相应步骤给分。

练习册系列答案
相关题目
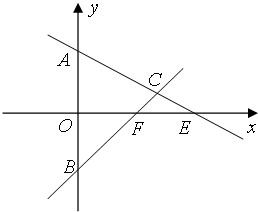 在△ABC中,已知A(0,1)、B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且
在△ABC中,已知A(0,1)、B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且 在△ABC中,已知A(0,1),B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且
在△ABC中,已知A(0,1),B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且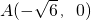 、
、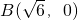 ,动点P满足|PA|=|PB|+4.
,动点P满足|PA|=|PB|+4.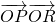 的值.
的值. 、
、 ,动点P满足|PA|=|PB|+4.
,动点P满足|PA|=|PB|+4.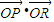 的值.
的值.