Question

在△ABC中，已知A（0，1），B（0，-1），AC、BC两边所在的直线分别与x轴交于E、F两点，且

OE

•

OF

=4．
（1）求点C的轨迹方程；
（2）若

BC

=-8

CF

，
①试确定点F的坐标；
②设P是点C的轨迹上的动点，猜想△PBF的周长最大时点P的位置，并证明你的猜想．

Answer 1

分析：（1）设出C的坐标，利用向量共线的充要条件及向量的数量积公式，列出关于点C的坐标的方程化简即得到得到点C的轨迹方程；
（2）①设出F的坐标，根据已知条件

BC

=-8

CF

，得到点F与点C的关系，表示出C的坐标，将其代入（1）中求出的方程得到F的坐标．
②先猜想当P点位于直线BF₁与椭圆的交点处时，△PBF周长最大，然后利用椭圆的定义加以证明．

解答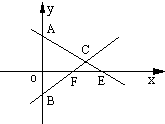：解：（1）如图，设点C（x，y）（x≠0），E（x_E，0），F（x_F，0），由A，C，F三点共线，

AC

•

AE

⇒x(-1)-(y-1)xE=0，
x_E=

x

1-y

．
同理，由B、C、F三点共线可得x_F=

x

1+y

．
∵

OE

•

OF

=4，
∴x_E•x_F=

x

1-y

•

x

1+y

=4．
化简，得点C的轨迹方程为x²+4y²=4（x≠0）．
（2）若

BC

=-8

CF

，
①设F（x_F，0），C（x_C，y_C），
∴

BC

=-8

CF

⇒（x_c，y_c+1）=-8（x_F-x_c，y_c）．
∴x_c=

8

7

xF，y_C=

1

7

．
代入x²+4y²=4，得x_F=±

3

．
∴F（±

3

，0），即F为椭圆的焦点．
②猜想：取F（

3

，0），设F₁（-

3

，0）是左焦点，
则当P点位于直线BF₁与椭圆的交点处时，△PBF周长最大，最大值为8．
证明如下：|PF|+|PB|=4-|PF₁|+|PB|≤4+|BF₁|，
∴△PBF的周长≤4+|BF₁|+|BF|≤8．

点评：本题考查利用向量解决圆锥曲线问题，求轨迹方程常用的方法有：直接法、相关点法、交轨法、消参法等，属于难题．