Question

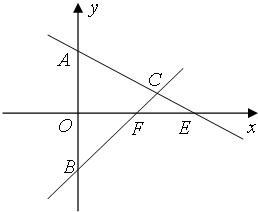在△ABC中，已知A（0，1）、B（0，-1），AC、BC两边所在的直线分别与x轴交于E、F两点，且

OE

•

OF

=4．
（I）求点C的轨迹方程；
（Ⅱ）若

BC

=-8

CF

，
①试确定点F的坐标；
②设P是点C的轨迹上的动点，猜想△PBF的周长最大时点P的位置．

Answer 1

分析：（1）设出点的坐标，根据三点共线得到坐标之间的关系，根据数量积为4，整理点C的坐标满足的关系，注意所求的曲线上的点是否都满足条件，把不合题意的去掉．
（2）根据向量之间的关系得到点之间的关系，把所求的点之间的关系代入曲线的方程的，得到点的坐标，猜想周长最大时P的位置，一般情况下是一个特殊点．

解答：解：（I）如图，设点C（x，y），E（x_E，0），F（x_f，0），
由A，C，E三点共线，
得

AC

•

AE

=x(-1)-(y-1)xE=0，
∴xE=

x

1-y

，
同理，由B、C、F三点共线可xF=

x

1+y

，
∵

OE

•

OF=4

∴x_E•x_F=4，
化简，得C的轨迹方程为

x2

4

+y2=1(x≠0)．

（Ⅱ）若

BC

=-8

CF

，
①∵

BC

=-8

CF

，
∴（x_c，y_c+1）=-8（x_f-x_c，-y_c）
∴xc=

8

7

xf，yc=

1

7

代入

x2

4

+y2=1，得xf=±

3

∴F(±

3

，0)
即F为椭圆的焦点．
②猜想：F₂（

3

，0)，F1 (-

3

，0)是椭圆左焦点，
则P点位于直线BF₁与椭圆的交点处时，
△BCF周长最大，最大值为8．

点评：通过向量的坐标表示实现向量问题代数化，注意与方程、函数等知识的联系，一般的向量问题的处理有两种思路，一种是纯向量式的，另一种是坐标式，两者互相补充．