题目内容
证明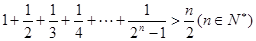 时,假设当
时,假设当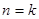 时成立,则当
时成立,则当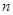
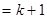 时,左边增加的项数为( )
时,左边增加的项数为( )
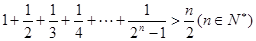 时,假设当
时,假设当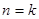 时成立,则当
时成立,则当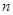
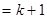 时,左边增加的项数为( )
时,左边增加的项数为( )A.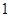 | B.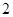  | C.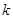 | D.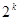 |
D
解:n=k时,不等式的左边等于 1+1 /2 +1 /3 +1 /4 +…+1 /(2k-1) ,且 k∈N+,
当n=k+1时,不等式的左边等于 1+1 /2 +1/ 3 +1/ 4 +…+1 /2k-1 +(1 /2k +1 /(2k+1) +1/ (2k +2) +…+1 /(2k +2k -1 )),
当n=k+1时,不等式的左边比n=k时增加的向为1 /2k +1 /(2k+1) +1/ (2k +2) +…+1 /(2k +2k -1 ) ,共增加了 2k项.
故选D.
当n=k+1时,不等式的左边等于 1+1 /2 +1/ 3 +1/ 4 +…+1 /2k-1 +(1 /2k +1 /(2k+1) +1/ (2k +2) +…+1 /(2k +2k -1 )),
当n=k+1时,不等式的左边比n=k时增加的向为1 /2k +1 /(2k+1) +1/ (2k +2) +…+1 /(2k +2k -1 ) ,共增加了 2k项.
故选D.

练习册系列答案
相关题目
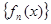 满足:
满足: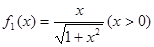 ,
,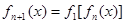
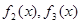 ;
;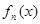 的表达式,并证明你的结论.
的表达式,并证明你的结论.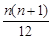 (an2+bn+c)
(an2+bn+c) 能够被6整除.
能够被6整除.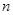 条两两相交的弦,把圆最多分成 部分.
条两两相交的弦,把圆最多分成 部分.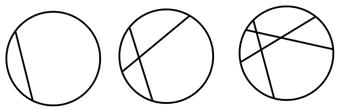
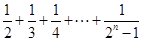 ,则n=k+1与n=k时相比,左边应添加( )
,则n=k+1与n=k时相比,左边应添加( )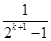
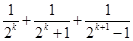
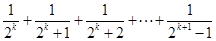
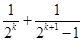
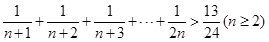 的过程中,由
的过程中,由 递推到
递推到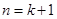 时的不等式左边.
时的不等式左边.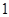 项
项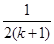
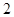 项
项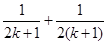
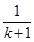 ”
”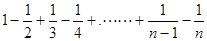 (n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.
(n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.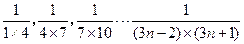 ,计算
,计算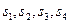 ,猜想
,猜想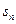 的表达式,并用数学归纳法证明猜想的正确性
的表达式,并用数学归纳法证明猜想的正确性