Question

已知双曲线

y2

16

-

x2

9

=1的上焦点为F，点A（1，6），在双曲线上求一点P，使得|PA|+

4

5

|PF|的值最小（　　）

• A．(1，

  4 10

  3

  )
• B．(1，-

  4 10

  3

  )
• C．(

  3 5

  2

  ，6)
• D．(-

  3 5

  2

  ，6)

Answer 1

分析：由双曲线

y2

16

-

x2

9

=1的离心率e=

5

4

，知

4

5

|PF|=|PB|，由此得到|PA|+

4

5

|PF|的值最小时的P点的坐标是过点A作准线的垂线与抛物线的上支的交点，从而能求出结果．

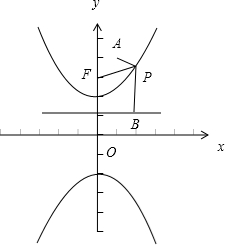解答：解：∵双曲线

y2

16

-

x2

9

=1的离心率e=

5

4

，
∴

|PF|

|PB|

=

5

4

，即

4

5

|PF|=|PB|，
∴|PA|+

4

5

|PF|的值最小时的P点的坐标是过点A作准线的垂线与抛物线的上支的交点，
∵A（1，6），∴设P（1，y），
把P（1，y）代入双曲线

y2

16

-

x2

9

=1，得

y2

16

-

1

9

=1，解得y=±

4 10

3

．
∴P（1，

4 10

3

）．
故选A．

点评：本题考查抛物线的性质的应用，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．