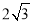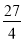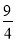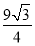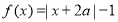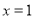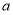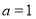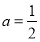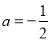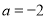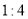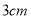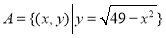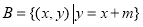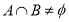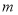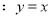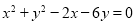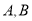题目内容
已知平面内两点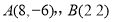 .
.
(1)求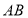 的中垂线方程;
的中垂线方程;
(2)求过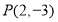 点且与直线
点且与直线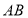 平行的直线
平行的直线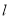 的方程;
的方程;
(3)一束光线从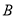 点射向(Ⅱ)中的直线
点射向(Ⅱ)中的直线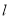 ,若反射光线过点
,若反射光线过点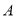 ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.
(1) 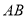 的中垂线方程为
的中垂线方程为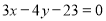 ;(2) 直线
;(2) 直线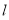 的方程
的方程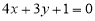 ;
;
(3) 反射光线所在的直线方程为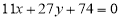 .
.
【解析】
试题分析:(1)先求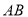 的中点坐标为
的中点坐标为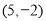 ,利用两直线垂直
,利用两直线垂直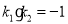 ,则
,则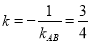 ,再利用点斜式写出直线方程即可;
,再利用点斜式写出直线方程即可;
(2)利用两直线平行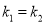 ,则
,则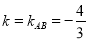 ,再利用点斜式写出直线方程即可;
,再利用点斜式写出直线方程即可;
(3)先利用点关于直线的对称点求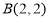 关于直线
关于直线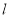 的对称点
的对称点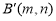 ,
,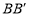 的中点在直线
的中点在直线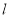 上,
上,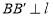 ,则斜率乘积为 1,联立方程可解
,则斜率乘积为 1,联立方程可解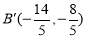 ,
, ,再利用点斜式写出直线方程即可.
,再利用点斜式写出直线方程即可.
试题解析:(1)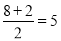 ,
,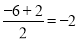 ,∴
,∴ 的中点坐标为
的中点坐标为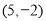 1分
1分
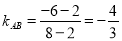 ,∴
,∴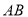 的中垂线斜率为
的中垂线斜率为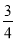 2分
2分
∴由点斜式可得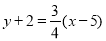 3分
3分
∴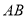 的中垂线方程为
的中垂线方程为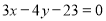 4分
4分
(2)由点斜式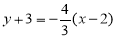 5分
5分
∴直线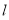 的方程
的方程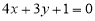 6分
6分
(3)设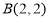 关于直线
关于直线 的对称点
的对称点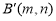 7分
7分
∴ , 8分
, 8分
解得 10分
10分
∴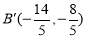 ,
, 11分
11分
由点斜式可得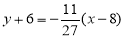 ,整理得
,整理得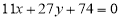
∴反射光线所在的直线方程为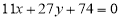 . 12分
. 12分
法二:设入射点的坐标为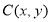
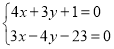 , 8分
, 8分
解得 10分
10分
∴ 11分
11分
由点斜式可得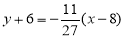 ,整理得
,整理得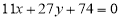
∴反射光线所在的直线方程为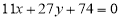 . 12分
. 12分
考点:本题考查直线的点斜式方程,直线平行、垂直的斜率关系;点关于直线的对称问题.