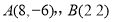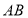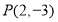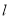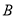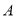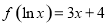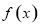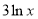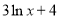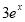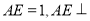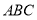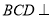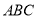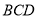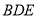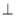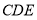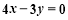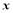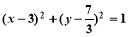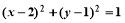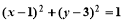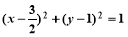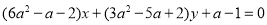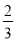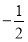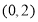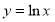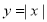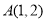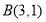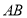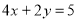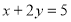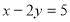题目内容
直线
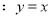 与圆
与圆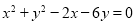 相交于
相交于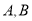 两点,则
两点,则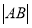 =________.
=________.
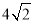
【解析】
试题分析:求圆的弦长,尤其独特方法,即利用圆半径、半弦长、圆心到弦所在直线距离构成直角三角形解决弦长问题.现将圆方程化为标准式: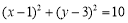 得圆心为
得圆心为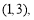 半径为
半径为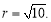 圆心到弦所在直线距离为
圆心到弦所在直线距离为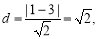 所以
所以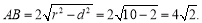 直线截曲线弦长问题通法是求交点,利用两点间距离公式解决.思路简单,但运算量较大.因此在涉及弦长问题时,通常考虑能否不求交点坐标而直接表示出弦长,如可利用韦达定理.
直线截曲线弦长问题通法是求交点,利用两点间距离公式解决.思路简单,但运算量较大.因此在涉及弦长问题时,通常考虑能否不求交点坐标而直接表示出弦长,如可利用韦达定理.
考点:直线与圆,圆的弦长,点到直线距离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目