题目内容
已知f(x)=x3+bx2+cx+d在(-∞,0)上是增函数,在[0,2]上是减函数,且方程f(x)=0有三个根,它们分别为α、2、β.(1)求c的值;(2)求证:f(1)≥2;(3)求|α-β|的取值范围.
解:(1)f′(x)=3x2+2bx+c.∵f(x)在(-∞,0)上是增函数,在[0,2]上是减函数,∴x=0时,f(x)取得极大值,∴f′(0)=0.即c=0,从而f(x)=x3+bx2+d.
(2)由题设f(2)=0,即d=-4(b+2),则f(1)=1+b+d=-7-3b.又
f′(x)=3x2+2bx,令f′(x)=0,得x1=0或x2=-![]() b.
b.
∵f(x)在[0,2]上是减函数,从而-![]() b≥2,即b≤-3,∴f(1)=-7-3b≥2.
b≥2,即b≤-3,∴f(1)=-7-3b≥2.
(3)∵α、2、β是f(x)=0的三个根,从而
f(x)=(x-α)(x-2)(x-β)=x3-(2+α+β)x2+(2a+2β+αβ)x-2αβ,
于是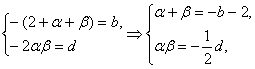
∴|α-β|=
![]()
∵b≤-3,∴|α-β|≥3.
说明:本题涉及到了三次方程的根与系数的关系:设一元三次方程ax3+bx2+cx+d=0的三个根为x1、x2、x3,则ax3+bx2+cx+d=a(x-x1)(x-x2)(x-x3)展开即可得到根x1、x2、x3与系数a、b、c、d的关系.

练习册系列答案
相关题目