题目内容
下列有关命题说法正确的是( )
A.命题p:“存在x∈R,sinx+cosx=
| ||
| B.“a=1”是“函数f(x)=cos2ax-sin2ax的周期T=π”的充分必要条件 | ||
| C.命题“存在x∈R,使得x2+x+1=0”的否定是:“对任意x∈R,x2+x+1≥0” | ||
D.命题“若tanα≠1,则α≠
|
A.命题p:“存在x∈R,sinx+cosx=
”,由于sinx+cosx=
sin(x+
)≤
,
因此命题p是假命题,故¬p是真命题,因此A不正确.
B.由函数f(x)=cos2ax-sin2ax=cos2ax,∴T=
=
=π,解得a=±1.
因此“a=1”是“函数f(x)=cos2ax-sin2ax的周期T=π”的充分但不必要条件.因此B不正确.
C.命题“存在x∈R,使得x2+x+1=0”的否定应是:“对任意x∈R,x2+x+1≠0”,因此不正确;
D.命题“若tanα≠1,则α≠
”的逆否命题是“若α=
,则tanα=1”是真命题.
故选:D.
| 3 |
| 2 |
| π |
| 4 |
| 2 |
因此命题p是假命题,故¬p是真命题,因此A不正确.
B.由函数f(x)=cos2ax-sin2ax=cos2ax,∴T=
| 2π |
| |2a| |
| π |
| |a| |
因此“a=1”是“函数f(x)=cos2ax-sin2ax的周期T=π”的充分但不必要条件.因此B不正确.
C.命题“存在x∈R,使得x2+x+1=0”的否定应是:“对任意x∈R,x2+x+1≠0”,因此不正确;
D.命题“若tanα≠1,则α≠
| π |
| 4 |
| π |
| 4 |
故选:D.

练习册系列答案
相关题目
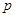 :“若
:“若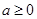 ,则
,则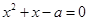 有实根”.
有实根”.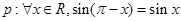 ;命题
;命题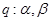 均是第一象限的角,且
均是第一象限的角,且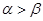 ,则
,则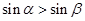 ,下列命题是真命题的是( )
,下列命题是真命题的是( )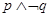
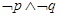
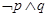
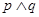
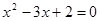 ,则
,则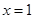 ”的逆否命题为“若
”的逆否命题为“若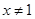 ,则
,则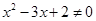 ”
”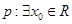 ,使得
,使得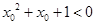 ,则
,则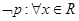 ,则
,则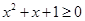
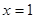 ”是“
”是“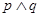 为假命题,则
为假命题,则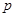 、
、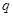 均为假命题
均为假命题