题目内容
若函数f(x)=sin2ax-sinaxcosax(a>0)的图象与直线y=m相切,并且切点的横坐标依次成公差为 的等差数列.
的等差数列.(1)求m的值.
(2)若点A(x,y)是y=f(x)图象的对称中心,且x∈[0,
 ],求点A的坐标.
],求点A的坐标.
【答案】分析:(1)利用二倍角公式将f(x)=sin2ax-sinaxcosax化为f(x)=-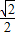 sin(2ax+
sin(2ax+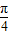 )+
)+ ,结合函数图象可得所以m为f(x)的最大值或最小值.
,结合函数图象可得所以m为f(x)的最大值或最小值.
(2)切点的横坐标依次成公差为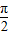 的等差数列.得出f(x)的最小正周期为
的等差数列.得出f(x)的最小正周期为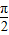 .从而a=2,确定出f(x)解析式.若点A(x,y)是y=f(x)图象的对称中心则应有y=0=f(x),利用特殊角的三角函数值解此方程求出x.
.从而a=2,确定出f(x)解析式.若点A(x,y)是y=f(x)图象的对称中心则应有y=0=f(x),利用特殊角的三角函数值解此方程求出x.
解答:解:(1)f(x)= (1-cos2ax)-
(1-cos2ax)- sin2ax
sin2ax
=- (sin2ax+cos2ax)+
(sin2ax+cos2ax)+ =-
=-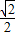 sin(2ax+
sin(2ax+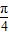 )+
)+
因为y=f(x)的图象与y=m相切.所以m为f(x)的最大值或最小值.
即m=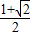 或m=
或m=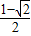 .
.
(2)因为切点的横坐标依次成公差为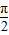 的等差数列,所以f(x)的最小正周期为
的等差数列,所以f(x)的最小正周期为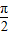 .
.
由T=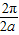 =
=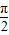 得a=2.
得a=2.
∴f(x)=-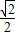 sin(4x+
sin(4x+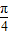 )+
)+ .
.
由sin(4x+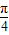 )=0得4x+
)=0得4x+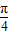 =kπ,即x=
=kπ,即x=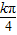 -
-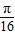 (k∈Z).
(k∈Z).
由0≤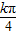 -
-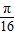 ≤
≤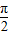 得k=1或k=2,
得k=1或k=2,
因此点A的坐标为(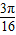 ,
, )或(
)或(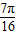 ,
, )
)
点评:本题考查三角函数公式的应用(包括正用,逆用)、三角函数图象及性质(最值、周期、对称点)、特殊角的三角函数值.需有转化、计算、方程的思想和能力.
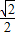 sin(2ax+
sin(2ax+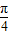 )+
)+ ,结合函数图象可得所以m为f(x)的最大值或最小值.
,结合函数图象可得所以m为f(x)的最大值或最小值.(2)切点的横坐标依次成公差为
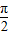 的等差数列.得出f(x)的最小正周期为
的等差数列.得出f(x)的最小正周期为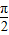 .从而a=2,确定出f(x)解析式.若点A(x,y)是y=f(x)图象的对称中心则应有y=0=f(x),利用特殊角的三角函数值解此方程求出x.
.从而a=2,确定出f(x)解析式.若点A(x,y)是y=f(x)图象的对称中心则应有y=0=f(x),利用特殊角的三角函数值解此方程求出x.解答:解:(1)f(x)=
 (1-cos2ax)-
(1-cos2ax)- sin2ax
sin2ax=-
 (sin2ax+cos2ax)+
(sin2ax+cos2ax)+ =-
=-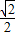 sin(2ax+
sin(2ax+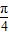 )+
)+
因为y=f(x)的图象与y=m相切.所以m为f(x)的最大值或最小值.
即m=
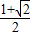 或m=
或m=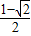 .
.(2)因为切点的横坐标依次成公差为
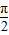 的等差数列,所以f(x)的最小正周期为
的等差数列,所以f(x)的最小正周期为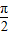 .
.由T=
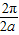 =
=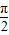 得a=2.
得a=2.∴f(x)=-
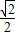 sin(4x+
sin(4x+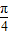 )+
)+ .
.由sin(4x+
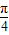 )=0得4x+
)=0得4x+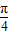 =kπ,即x=
=kπ,即x=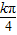 -
-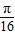 (k∈Z).
(k∈Z).由0≤
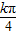 -
-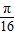 ≤
≤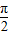 得k=1或k=2,
得k=1或k=2,因此点A的坐标为(
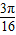 ,
, )或(
)或(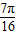 ,
, )
)点评:本题考查三角函数公式的应用(包括正用,逆用)、三角函数图象及性质(最值、周期、对称点)、特殊角的三角函数值.需有转化、计算、方程的思想和能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
设|φ|<
,函数f(x)=sin2(x+φ).若f(
)=
,则φ等于( )
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
 )-
)- ,则函数f(x)是( )
,则函数f(x)是( )