题目内容
.设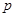 :函数
:函数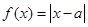 在区间
在区间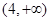 上单调递增;
上单调递增;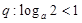 ,如果“
,如果“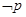 ”是真命题,
”是真命题, 也是真命题,求实数
也是真命题,求实数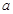 的取值范围.
的取值范围.
【答案】
解:p: ∵f(x)=|x-a|在区间(4,+∞)上递增
故a≤4.
q:由loga2<1=logaa得0<a<1或a>2.
如果“┐p”为真命题,则p为假命题,即a>4.
又q为真,即0<a<1或a>2
由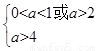 可得实数a的取值范围是a>4
可得实数a的取值范围是a>4
【解析】略

练习册系列答案
相关题目
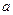 是实数,设函数
是实数,设函数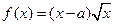
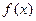 的单调性;
的单调性;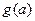 为函数
为函数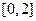 上的最小值
上的最小值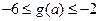
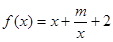 (
(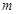 为实常数).
为实常数).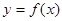 图像上动点
图像上动点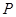 到定点
到定点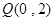 的距离的最小值为
的距离的最小值为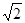 ,求实数
,求实数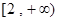 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数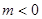 ,若不等式
,若不等式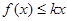 在
在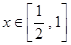 有解,求
有解,求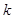 的取值范围.
的取值范围.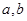 是实数,函数
是实数,函数 ,
,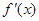 和
和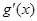 ,分别是
,分别是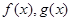 的导函数,若
的导函数,若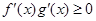 在区间
在区间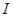 上恒成立,则称
上恒成立,则称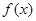 和
和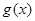 在区间
在区间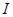 上单调性一致.
上单调性一致.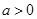 ,若函数
,若函数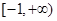 上单调性一致,求实数
上单调性一致,求实数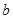 的取值范围;
的取值范围;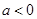 且
且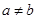 ,若函数
,若函数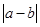 的最大值.
的最大值.
 和
和 是
是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 ,若
,若 上单调性一致,求b的取值范围;
上单调性一致,求b的取值范围; 且
且 ,若
,若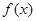 是定义在R的奇函数,当
是定义在R的奇函数,当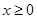 时,
时,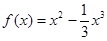 .
.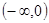 上的单调性;
上的单调性;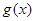 是函数
是函数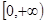 上的导函数,问是否存在实数
上的导函数,问是否存在实数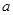 ,满足
,满足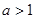 并且使
并且使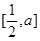 上的值域为
上的值域为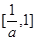 ,若存在,求出
,若存在,求出