题目内容
(满分12分)已知a,b是实数,函数
 和
和 是
是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 上单调性一致
上单调性一致
(1)设 ,若
,若 和
和 在区间
在区间 上单调性一致,求b的取值范围;
上单调性一致,求b的取值范围;
(2)设 且
且 ,若
,若 和
和 在以a,b为端点的开区间上单调性一致,
在以a,b为端点的开区间上单调性一致,
求|a―b|的最大值
【答案】
(1) (2)
(2)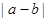 的最大值为
的最大值为
【解析】本试题主要是考查了导数在研究函数中的运用
(1)根据新的定义,单调性一致的理解,可知只要导函数的乘积为非负数即可,这样可以得到参数的取值范围。
(2)根据函数在给定区间上单调性一致,可以构造函数的思想,结合导数的符号来判定函数的单调性质,进而得到区间端点值的差的绝对值的最大值。
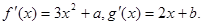
(1)由题意知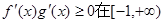 上恒成立,因为a>0,故
上恒成立,因为a>0,故
进而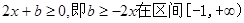 上恒成立,所以
上恒成立,所以 因此
因此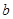 的取值范围是
的取值范围是
(2)令
若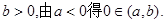 又因为
又因为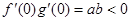 ,
,
所以函数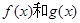 在
在 上不是单调性一致的,因此
上不是单调性一致的,因此
现设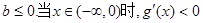 ;
;
当 时,
时,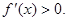
因此,当 时,
时,
故由题设得
从而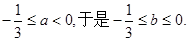
因此 时等号成立,
时等号成立,
又当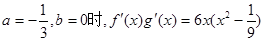 ,从而当
,从而当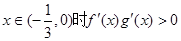
故当函数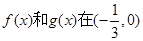 上单调性一致,因此
上单调性一致,因此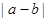 的最大值为
的最大值为

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
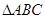 的三个内角且向量
的三个内角且向量 共线。
共线。 的对边分别是
的对边分别是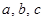 ,且满足
,且满足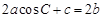 ,试判断
,试判断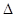
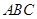 的形状.
的形状.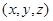 中的
中的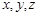 分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组
分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组 ,b
,b .
.
 ,求
,求 的值;
的值; 的值.
的值.