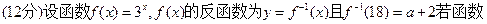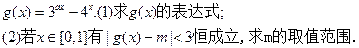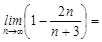题目内容
解答下列问题:
(1)若f(x+1)=2x2+1,求f(x);
(2)若2f(x)-f(-x)=x+1,求f(x);
(3)若函数f(x)=
,f(2)=1,且方程f(x)=x有唯一解,求f(x).
(1)若f(x+1)=2x2+1,求f(x);
(2)若2f(x)-f(-x)=x+1,求f(x);
(3)若函数f(x)=
| x |
| ax+b |
(1)令x+1=t,则x=t-1,所以f(t)=2(t-1)2+1=2t2-4t+3,即f(x)=2x2-4x+3;
(2)由2f(x)-f(-x)=x+1①,取x=-x,代入该式得:2f(-x)-f(x)=-x+1②,
联立①②得:f(x)=
x+1;
(3)因为函数f(x)=
,由f(2)=1得:
=1③
由方程f(x)=x有唯一解,即
=x有唯一解,
也就是ax2+(b-1)x=0有唯一解,
当a=0时,由③得b=2.
当a≠0时,则有(b-1)2=0,所以b=1,代入③得:a=
所以f(x)=
或f(x)=
.
(2)由2f(x)-f(-x)=x+1①,取x=-x,代入该式得:2f(-x)-f(x)=-x+1②,
联立①②得:f(x)=
| 1 |
| 3 |
(3)因为函数f(x)=
| x |
| ax+b |
| 2 |
| 2a+b |
由方程f(x)=x有唯一解,即
| x |
| ax+b |
也就是ax2+(b-1)x=0有唯一解,
当a=0时,由③得b=2.
当a≠0时,则有(b-1)2=0,所以b=1,代入③得:a=
| 1 |
| 2 |
所以f(x)=
| x |
| 2 |
| 2x |
| x+2 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
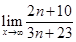 = .
= . +1,则
+1,则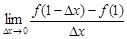 的值为 ( )
的值为 ( )