题目内容
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
则在犯错误的概率不超过 的前提下认为喜爱打篮球与性别有关(请用百分数表示).
附:χ2=
| | 喜爱打篮球 | 不喜爱打篮球 | 总计 |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 总计 | 30 | 20 | 50 |
附:χ2=

| P(χ2≥x0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
0.5%
χ2=
=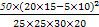 ≈8.333>7.879,所以在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
≈8.333>7.879,所以在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
【方法技巧】两个分类变量是否有关的直观判断
在列联表中,可以估计满足条件X=x1的个体中具有Y=y1的个体所占的比重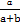 ,和满足条件X=x2的个体中具有Y=y1的个体所占的比重
,和满足条件X=x2的个体中具有Y=y1的个体所占的比重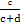 ,若两个分类变量无关,则两个比重应差别不大,即
,若两个分类变量无关,则两个比重应差别不大,即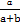 ≈
≈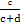 ,因此两个比重
,因此两个比重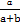 和
和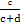 相差越大,两个分类变量有关的可能性就越大.
相差越大,两个分类变量有关的可能性就越大.

=
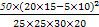 ≈8.333>7.879,所以在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
≈8.333>7.879,所以在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.【方法技巧】两个分类变量是否有关的直观判断
在列联表中,可以估计满足条件X=x1的个体中具有Y=y1的个体所占的比重
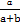 ,和满足条件X=x2的个体中具有Y=y1的个体所占的比重
,和满足条件X=x2的个体中具有Y=y1的个体所占的比重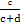 ,若两个分类变量无关,则两个比重应差别不大,即
,若两个分类变量无关,则两个比重应差别不大,即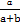 ≈
≈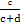 ,因此两个比重
,因此两个比重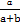 和
和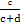 相差越大,两个分类变量有关的可能性就越大.
相差越大,两个分类变量有关的可能性就越大.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
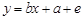 中,下列说法正确的是( )
中,下列说法正确的是( )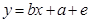 是一次函数
是一次函数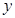 是由自变量
是由自变量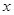 唯一确定的
唯一确定的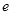 的产生
的产生 算得,
算得, ≈7.8.
≈7.8.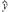 =
= x+
x+ ,求得
,求得 =61.75,
=61.75, =38.14,则线性回归方程为( )
=38.14,则线性回归方程为( ) =-3.2x+
=-3.2x+ 则实数
则实数 .
.
 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 ,a=y-bx
,a=y-bx