题目内容
已知双曲线C与椭圆
+
=1有相同的焦点,实半轴长为
.
(1)求双曲线C的方程;
(2)若直线l:y=kx+
与双曲线C有两个不同的交点A和B,且
•
>2(其中O为原点),求k的取值范围.
| x2 |
| 8 |
| y2 |
| 4 |
| 3 |
(1)求双曲线C的方程;
(2)若直线l:y=kx+
| 2 |
| OA |
| OB |
分析:(1)设双曲线的方程为
-
=1(a>0,b>0),由已知易求a,c,根据a,b,c的平方关系即可求得b值;
(2)设A(x1,y1),B(x2,y2),则由
•
>2,可得x1x2+y1y2=x1x2+(kx1+
)(kx2+
)=(k2+1)x1x2+
k(x1+x2)+2>2,联立方程组消掉y,根据韦达定理即可得到关于k的不等式,注意判别式大于0,解出即得k的范围.
| x2 |
| a2 |
| y2 |
| b2 |
(2)设A(x1,y1),B(x2,y2),则由
| OA |
| OB |
| 2 |
| 2 |
| 2 |
解答:解:(1)设双曲线的方程为
-
=1(a>0,b>0),
由题意知,a=
,c=2,∴b2=c2-a2=1,解得b=1,
故双曲线方程为
-y2=1.
(2)将y=kx+
代入
-y2=1,得(1-3k2)x2-6
kx-9=0
由
得k2≠
,且k2<1,x1+x2=
,x1x2=
,
设A(x1,y1),B(x2,y2),则由
•
>2,
得x1x2+y1y2=x1x2+(kx1+
)(kx2+
)=(k2+1)x1x2+
k(x1+x2)+2=(k2+1)
+
k
+2>2,得
<k2<3.
又k2<1,∴
<k2<1,解得k∈(-1,-
)∪(
,1),
所以k的取值范围为(-1,-
)∪(
,1).
| x2 |
| a2 |
| y2 |
| b2 |
由题意知,a=
| 3 |
故双曲线方程为
| x2 |
| 3 |
(2)将y=kx+
| 2 |
| x2 |
| 3 |
| 2 |
由
|
| 1 |
| 3 |
6
| ||
| 1-3k2 |
| -9 |
| 1-3k2 |
设A(x1,y1),B(x2,y2),则由
| OA |
| OB |
得x1x2+y1y2=x1x2+(kx1+
| 2 |
| 2 |
| 2 |
| -9 |
| 1-3k2 |
| 2 |
6
| ||
| 1-3k2 |
| 1 |
| 3 |
又k2<1,∴
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |
所以k的取值范围为(-1,-
| ||
| 3 |
| ||
| 3 |
点评:本题考查直线与圆锥曲线的位置关系及双曲线标准方程的求解,考查向量数量积运算及韦达定理的应用,考查学生的运算能力及对问题转化能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
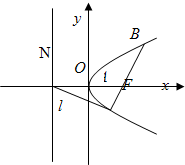 已知双曲线C:y2-x2=8,直线l:y=-x+8,若椭圆M与双曲线C有公共焦点,与直线l有公共点P,求椭圆长轴的最小值及此时P点的坐标.
已知双曲线C:y2-x2=8,直线l:y=-x+8,若椭圆M与双曲线C有公共焦点,与直线l有公共点P,求椭圆长轴的最小值及此时P点的坐标.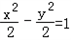 ,椭圆方程
,椭圆方程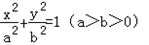 ,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,
,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,