题目内容
已知双曲线C的方程为x2-y2=4,椭圆E以双曲线C的顶点为焦点,且椭圆右顶点A到双曲线C的渐近线距离为3.(1)求椭圆E的方程;
(2)若直线y=x与椭圆E交于M、N两点(M点在第一象限),P、Q是椭圆上不同于M的相异两点,并且∠PMQ的平分线垂直于x轴.试求直线PQ的斜率.
解:(1)设椭圆的方程为![]() +
+![]() =1(a>b>0),由题意
=1(a>b>0),由题意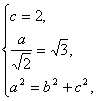 解得
解得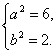
因此,椭圆的方程为![]() =1.
=1.
(2)由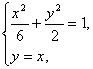 解之得
解之得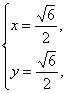 或
或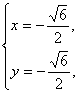 ∴M(
∴M(![]() ,
,![]() ).
).
若PM斜率存在,∵∠PMQ的平分线垂直于x轴,
设PM的斜率为k,则QM的斜率为-k,因此PM和QM的方程分别为
y=k(x![]() )+
)+![]() ,y=-k(x
,y=-k(x![]() )+
)+![]() ,由
,由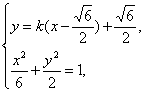
消去y并整理得(1+3k2)x2-3![]() k(k-1)x+
k(k-1)x+![]() k2-9k
k2-9k![]() =0(*).
=0(*).
∵M(![]() ,
,![]() )在椭圆上,∴x=
)在椭圆上,∴x=![]() 是方程(*)的一个根.
是方程(*)的一个根.
从而xP=![]() ,同理xQ=
,同理xQ=![]() ,
,
从而直线PQ的斜率:kPQ=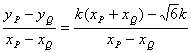 =
=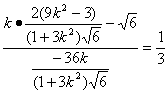 .
.
直线PQ的斜率为![]() .若直线PM的斜率不存在,则点Q、M重合,与题设不符.
.若直线PM的斜率不存在,则点Q、M重合,与题设不符.
综上所述,直线PQ的斜率为定值![]() .
.

练习册系列答案
相关题目