题目内容
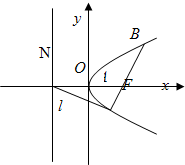 已知双曲线C:y2-x2=8,直线l:y=-x+8,若椭圆M与双曲线C有公共焦点,与直线l有公共点P,求椭圆长轴的最小值及此时P点的坐标.
已知双曲线C:y2-x2=8,直线l:y=-x+8,若椭圆M与双曲线C有公共焦点,与直线l有公共点P,求椭圆长轴的最小值及此时P点的坐标.分析:求出双曲线与椭圆的公共焦点,根据焦点设出椭圆的方程,将直线与椭圆的方程联立,消去x,令判别式大于等于0求出a的范围,即得到椭圆的长轴的长的最小值,进一步求出点p的坐标及直线的方程.
解答:解:双曲线C:y2-x2=8与椭圆M的公共焦点(0,±4),
可设椭圆的方程为
+
=1
联立:
⇒(2a2-16)x2-16(a2-16)x+(64-a2)(a2-16)=0
由于椭圆与直线l有公共点P,故△=162(a2-16)2-4(2a2-16)(64-a2)(a2-16)≥0
解得:a≥2
,故长轴2a最小值为4
此时,上述方程为x2-6x+9=0,得:x=3
代入l方程为y=5,因此P(3,5)
可设椭圆的方程为
| y2 |
| a2 |
| x2 |
| a2-16 |
联立:
|
由于椭圆与直线l有公共点P,故△=162(a2-16)2-4(2a2-16)(64-a2)(a2-16)≥0
解得:a≥2
| 10 |
| 10 |
此时,上述方程为x2-6x+9=0,得:x=3
代入l方程为y=5,因此P(3,5)
点评:解决直线与圆锥曲线的位置关系的问题,常用的方法是将直线的方程与圆锥曲线的方程联立来解决.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
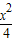 -y2=1,P是C上的任意点.
-y2=1,P是C上的任意点.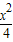 -y2=1,P是C上的任意点.
-y2=1,P是C上的任意点.