题目内容
(本小题满分12分)、已知函数 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,得到函数
个单位后,得到函数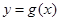 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
【答案】
(Ⅰ) 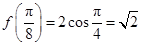 .
.
(Ⅱ)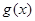 的单调递减区间为
的单调递减区间为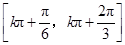 (
(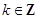 ).
).
【解析】本题主要考查了三角函数的恒等变换和三角函数图象的应用.属基础题.
(Ⅰ)先用两角和公式对函数f(x)的表达式化简得f(x)=2sin(ωx+φ- 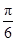 ),利用偶函数的性质即f(x)=f(-x)求得ω,进而求出f(x)的表达式,把x=
),利用偶函数的性质即f(x)=f(-x)求得ω,进而求出f(x)的表达式,把x= 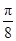 代入即可.
代入即可.
(Ⅱ)根据三角函数图象的变化可得函数g(x)的解析式,再根据余弦函数的单调性求得函数g(x)的单调区间
解:(Ⅰ)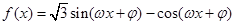
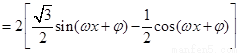
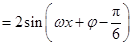 .……………………1分
.……………………1分
因为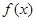 为偶函数,
为偶函数,
所以对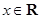 ,
,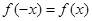 恒成立,
恒成立,
因此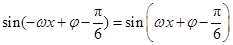 .……………………2分
.……………………2分
即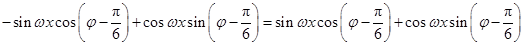 ,
,
整理得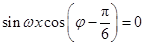 .因为
.因为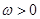 ,且
,且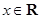 ,
,
所以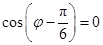 ……………………3分
……………………3分
又因为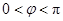 ,
,
故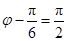 .
.
所以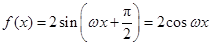 ……………………4分.
……………………4分.
由题意得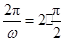 ,所以
,所以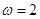 .
.
故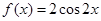 .……………………5分
.……………………5分
因此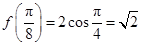 .……………………6分
.……………………6分
(Ⅱ)将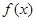 的图象向右平移
的图象向右平移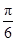 个单位后,得到
个单位后,得到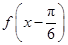 的图象,
的图象,
所以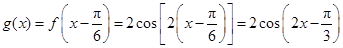 .……………………8分
.……………………8分
当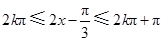 (
(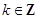 ),……………………10分
),……………………10分
即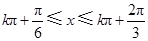 (
(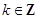 )时,
)时,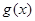 单调递减,
单调递减,
因此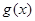 的单调递减区间为
的单调递减区间为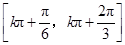 (
(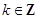 ).……………………12分
).……………………12分

练习册系列答案
相关题目