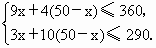题目内容
某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品,需要甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你给设计出来.
(2)设生产A、B两种产品获总利润为y(元),其中一种的生产件数为x,试写出y与x之间的函数关系式,并利用函数的性质说明(1)中哪些生产方案获总利润最大?最大利润是多少?
答案:略
解析:
解析:
|
(1) 设安排生产A种产品x件,则生产B种产品为(50-x)件,依题意,得
∵ x是整数,∴只能取30,31,32.∴生产方案有三种,分别为 A种30件,B种20件;A种31件,B种19件;A种32件,B种18件.(2) 设生产A种产品为x件,则y=700x+1200(50-x)=-500x+60000.∵ k=-500<0,∴y随x的增大而减小.∴当 x=30时,y值最大.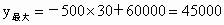 . .
∴安排生产 A种产品30件,B种产品20件时,获利利润最大,最大利润是45000元.要注意 (2)问与第(1)问的相互联系. |

练习册系列答案
相关题目