题目内容
某工厂生产甲、乙两种产品，这两种产品每千克的产值分别为600元和400元，已知每生产1千克甲产品需要A种原料4千克，B种原料2千克；每生产1千克乙产品需要A种原料2千克，B种原料3千克．但该厂现有A种原料100千克，B种原料120千克．问如何安排生产可以取得最大产值，并求出最大产值．
【答案】分析：先设生产甲、乙两种产品分别为x千克，y千克，其利产值为z元，列出约束条件，再根据约束条件画出可行域，设z=600x+400y，再利用z的几何意义求最值，只需求出直线z=600x+400y过可行域内的点时，从而得到z值即可．
解答：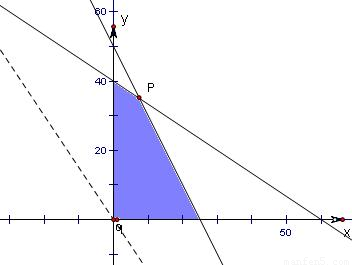
解析：设生产甲、乙两种产品分别为x千克，y千克，其利产值为z元，
根据题意，可得约束条件为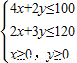
…（3分）
作出可行域如图：…．（5分）
目标函数z=600x+400y，
作直线l：3x+2y=0，再作一组平行于l的直线l：3x+2y=z，当直线l经过P点时z=600x+400y取得最大值，…．（9分）
由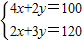
，解得交点P（ 7.5，35）…．（12分）
所以有z最大=600×7.5+400×35=18500（元）…（13分）
所以生产甲产品7.5千克，乙产品35千克时，总产值最大，为18500元．…（14分）
点评：本题是一道方案设计题型，考查了列一元一次不等式组解实际问题的运用及一元一次不等式组的解法的运用，解答时找到题意中的不相等关系是建立不等式组的关键．
解答：
解析：设生产甲、乙两种产品分别为x千克，y千克，其利产值为z元，根据题意，可得约束条件为
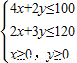…（3分）作出可行域如图：…．（5分）
目标函数z=600x+400y，
作直线l：3x+2y=0，再作一组平行于l的直线l：3x+2y=z，当直线l经过P点时z=600x+400y取得最大值，…．（9分）
由
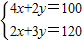，解得交点P（ 7.5，35）…．（12分）所以有z最大=600×7.5+400×35=18500（元）…（13分）
所以生产甲产品7.5千克，乙产品35千克时，总产值最大，为18500元．…（14分）
点评：本题是一道方案设计题型，考查了列一元一次不等式组解实际问题的运用及一元一次不等式组的解法的运用，解答时找到题意中的不相等关系是建立不等式组的关键．
练习册系列答案
相关题目
18、某工厂生产甲、乙两种产品，每种产品都是经过第一道和第二道工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级，对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品