题目内容
设A,B分别是直线y=(1)求轨迹C的方程;
(2)M,N是曲线C上的任意两点,且直线MN不与y轴垂直,线段MN的中垂线l交y轴于点E(0,y0),求y0的取值范围.
解:(1)设P(x,y),因为A、B分别为直线y=![]() x和y=-
x和y=-![]() x上的点,故可设A(x1 ,
x上的点,故可设A(x1 , ![]() x1),B(x2 ,
x1),B(x2 ,![]() x2).∵
x2).∵![]() =
=![]() +
+![]() ,∴
,∴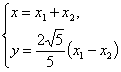
∴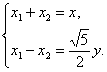 又
又![]() ,?
,?
∴(x1-x2)2+![]() (x1+x2)=20.?
(x1+x2)=20.?
∴![]() .即曲线C的方程为
.即曲线C的方程为![]() .?
.?
(2)设直线MN为y=kx+b(k≠0),则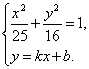 消去y,得(25k2+16)x2+50kbx+25(b2-16)=0.(*)由于M、N是曲线C上的任意两点,?
消去y,得(25k2+16)x2+50kbx+25(b2-16)=0.(*)由于M、N是曲线C上的任意两点,?
∴Δ=(50kb)2-4×25(25k 2+16)(b 2-16)>0.即25k 2b 2-(25k 2+16)(b 2-16)>0.∴b 2<25k2+16.①由(*)式可得![]() ,则直线l为
,则直线l为![]() .由于E(0,y0)在l上 ,∴
.由于E(0,y0)在l上 ,∴![]() .②由②得
.②由②得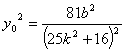 .代入①得
.代入①得![]() .∴-
.∴-![]() .即y0的取值范围是(
.即y0的取值范围是(![]() ,
,![]() ).
).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目