题目内容
(文科)设A、B分别是直线y=
x和y=-
x上的两个动点,并且|
|=
,满足
=
+
.(1)求动点P的轨迹C的方程;
(2)若点D的坐标为(0,16),M、N是曲线C上的两个动点,且
=λ
(λ≠1),求实数λ的取值范围.
2
| ||
| 5 |
2
| ||
| 5 |
| AB |
| 20 |
| OP |
| OA |
| OB |
(2)若点D的坐标为(0,16),M、N是曲线C上的两个动点,且
| DM |
| DN |
分析:(1)设动点P(x,y),再由题意设出A、B的坐标,根据
=
+
列出坐标之间的关系,再由|
|=
和向量模的公式,列出关于x和y的关系式,化简后得到所求的轨迹方程;
(2)设N(s,t),M(x,y),由
=λ
和D的坐标列出方程组,用s和t来表示x和y,再代入曲线方程消去s,求出t有关λ的表达式,再由|t|≤4求出λ的不等式.
| OP |
| OA |
| OB |
| AB |
| 20 |
(2)设N(s,t),M(x,y),由
| DM |
| DN |
解答:解:(1)设P(x,y),
由题可令A(x1,
x1),B(x2,-
x2),
∵
=
+
,
∴
即
又∵|
|=
,
∴(x1-x2)2+
(x1+x2)2=20,即有
y2+
x2=20.
∴轨迹C的方程为
+
=1
(2)设N(s,t),M(x,y),
则由
=λ
可得,(x,y-16)=λ(s,t-16),故x=λs,y=16+λ(t-16),
∵N、M在曲线C上,
∴
消去s得,
+
=1.
∵λ≠0且λ≠1,
∴t=
又∵|t|≤4,
∴|
|≤4,解得
≤λ≤
(λ≠1)
故实数λ的取值范围为
≤λ≤
(λ≠1).
由题可令A(x1,
2
| ||
| 5 |
2
| ||
| 5 |
∵
| OP |
| OA |
| OB |
∴
|
|
又∵|
| AB |
| 20 |
∴(x1-x2)2+
| 4 |
| 5 |
| 5 |
| 4 |
| 4 |
| 5 |
∴轨迹C的方程为
| x2 |
| 25 |
| y2 |
| 16 |
(2)设N(s,t),M(x,y),
则由
| DM |
| DN |
∵N、M在曲线C上,
∴
|
消去s得,
| λ2(16-t2) |
| 16 |
| (λt-16λ+16)2 |
| 16 |
∵λ≠0且λ≠1,
∴t=
| 17λ-15 |
| 2λ |
又∵|t|≤4,
∴|
| 17λ-15 |
| 2λ |
| 3 |
| 5 |
| 5 |
| 3 |
故实数λ的取值范围为
| 3 |
| 5 |
| 5 |
| 3 |
点评:本题主要考查了求轨迹方程和椭圆性质的综合应用.解题的前提是要求学生对基础知识有相当熟练的把握.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
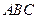 中,
中,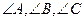 所对的边分别为
所对的边分别为 ,满足
,满足 成等差数列,
成等差数列, ,求点
,求点 的轨迹方程.
的轨迹方程. .
.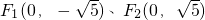 ,动点P满足条件:
,动点P满足条件: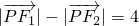 ,设点P的轨迹是曲线E,O为坐标原点.
,设点P的轨迹是曲线E,O为坐标原点.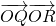 的取值范围;
的取值范围;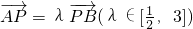 ,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.
,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.