��Ŀ����
����С������12�֣�
��ͼ��ABCD�������οյأ������εı߳�Ϊ30m����Դ�ڵ�P������P����AD��AB�ľ���ֱ�Ϊ9m��3m��ij��湫˾�ƻ��ڴ˿յ�����һ�鳤����Һ�������ĻMNEF��MN��NE=16��9���߶�MN�������P������M��N�ֱ��ڱ�AD��AB�ϣ���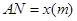 ��Һ�������ĻMNEF�����Ϊ
��Һ�������ĻMNEF�����Ϊ
��I����S����x�ĺ�����ϵʽ����д���ú����Ķ�����
��II����xȡ��ֵʱ��Һ�������ĻMNEF�����S��С��

���𰸡�
�⣺��I����ͼ������ֱ������ϵ����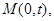
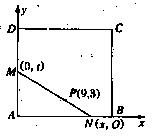
����֪��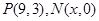
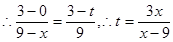
��MN����Dʱ��x��СֵΪ10��
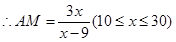 ��������2��
��������2��
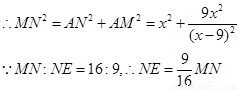
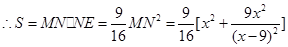 ��������5��
��������5��
������Ϊ[10��30] ��������6��
��II��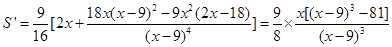
��������7��
��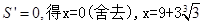 ��
��
��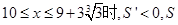 ����x��������
����x��������
��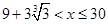 ʱ��
ʱ��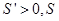 ����
����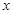 ������ ��������11��
������ ��������11��
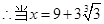 ʱ��Sȡ����Сֵ ��������11��
ʱ��Sȡ����Сֵ ��������11��
�𣺵�AN��Ϊ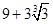 ��m��ʱ��Һ�������ĻMNEF�����S��С
��m��ʱ��Һ�������ĻMNEF�����S��С
��������12��
����������

��ϰ��ϵ�д�
�����Ŀ