题目内容
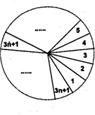 一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P
一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P
- A.随着n值的增大而减小且
 <p≤
<p≤
- B.是一个与n无关且落在区间(
 ,
, ]内的定值
]内的定值 - C.随着n值的增大而增大且
 ≤p<
≤p<
- D.是一个与n无关且落在区间,[
 ,
, )内的定值
)内的定值
C
分析:本题属于古典概型.欲求代号属于集合{4,7,10,…,3n+1)的概率,只须求出代号属于集合{4,7,10,…,3n+1)的对应区域的个数,以及整个事件对应的区域个数,最后求出它们的比值即得.
解答:∵标上1,2,3,…,3n+1中的一个数字(不重复)区域一共有3n+1的,
其中满足属于集合{4,7,10,…,3n+1)的有n个,
故属于集合{4,7,10,…,3n+1)的概率P=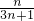 ,
,
它随着n值的增大而增大,且
∴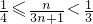
故选C.
点评:本题考查的知识点是几何概型的意义,几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=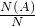 求解.
求解.
分析:本题属于古典概型.欲求代号属于集合{4,7,10,…,3n+1)的概率,只须求出代号属于集合{4,7,10,…,3n+1)的对应区域的个数,以及整个事件对应的区域个数,最后求出它们的比值即得.
解答:∵标上1,2,3,…,3n+1中的一个数字(不重复)区域一共有3n+1的,
其中满足属于集合{4,7,10,…,3n+1)的有n个,
故属于集合{4,7,10,…,3n+1)的概率P=
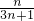 ,
,它随着n值的增大而增大,且
∴
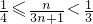
故选C.
点评:本题考查的知识点是几何概型的意义,几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
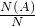 求解.
求解. 
练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
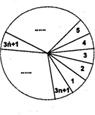 一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P( )
一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P( )A、随着n值的增大而减小且
| ||||
B、是一个与n无关且落在区间(
| ||||
C、随着n值的增大而增大且
| ||||
D、是一个与n无关且落在区间,[
|
 (2013•泰州三模)如图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的
(2013•泰州三模)如图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的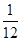 ,
,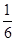 ,
,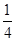 ,
,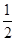 .游戏规则如下:
.游戏规则如下: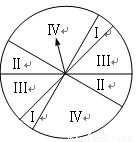
 .
.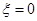 的概率;
的概率;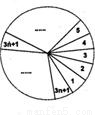
 <p≤
<p≤
 ,
, ]内的定值
]内的定值 ≤p<
≤p<
 ,
, )内的定值
)内的定值