题目内容
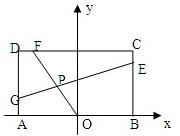 已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且| BE |
| BC |
| CF |
| CD |
| DG |
| DA |
分析:建立坐标系,按题意写出A,B,C,D四点的坐标,进而根据
=
=
解出E,F,G三点的坐标 参数表示,求出OF与GE两条直线的方程,两者联立即可求出点P的坐标满足的参数方程,消去参数,得到点P的轨迹方程.由于参数a的取值范围影响曲线的形状故按参数a的范围来对曲线进行分类.
| BE |
| BC |
| CF |
| CD |
| DG |
| DA |
解答:解:根据题设条件,首先求出点P坐标满足的方程,
据此再判断是否存在两定点,使得点P到定点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)
设
=
=
=k(0≤k≤1),
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为:2ax+(2k-1)y=0,①
直线GE的方程为:-a(2k-1)x+y-2a=0. ②
从①,②消去参数k,
得点P(x,y)坐标满足方程2a2x2+y2-2ay=0,
整理得
+
=1.
当a2=
时,点P的轨迹为圆弧,所以不存在符合题意的两点;
当a2≠
时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长;
当a2<
时,点P到椭圆两个焦点(-
,a),(
,a)的距离之和为定值
;
当a2>
时,点P到椭圆两个焦点(0,a-
),(0,a+
)的距离之和为定值2a.
据此再判断是否存在两定点,使得点P到定点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)
设
| BE |
| BC |
| CF |
| CD |
| DG |
| DA |
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为:2ax+(2k-1)y=0,①
直线GE的方程为:-a(2k-1)x+y-2a=0. ②
从①,②消去参数k,
得点P(x,y)坐标满足方程2a2x2+y2-2ay=0,
整理得
| x2 | ||
|
| (y-a)2 |
| a2 |
当a2=
| 1 |
| 2 |
当a2≠
| 1 |
| 2 |
当a2<
| 1 |
| 2 |
|
|
| 2 |
当a2>
| 1 |
| 2 |
a2-
|
a2-
|
点评:考查解析法求点的轨迹方程,本题在做题时引入了参数k,故得到的轨迹方程为参数方程,需要消去参数得到轨迹方程,又当字母的取值范围对曲线的形状有影响时,要对其范围进行讨论以确定轨迹的具体性状.考查分类讨论的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
如图,已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且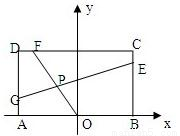 已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且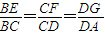 ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.