题目内容
(12分)定义![]() 的“倒平均数”为
的“倒平均数”为![]() ,已知数列
,已知数列![]() 前
前![]() 项的“倒平均数”为
项的“倒平均数”为![]() .
.
(1)记![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(2)是否存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 对任意
对任意![]() 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数![]() ;若不存在,说明理由.
;若不存在,说明理由.
解析:(1)记数列![]() 的前
的前![]() 项和为
项和为![]() ,则依题有
,则依题有![]()
![]() ,故
,故![]()
故数列的通项为![]() .故
.故![]() ,易知,
,易知,![]() .
.
(2)假设存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() 对任意
对任意![]() 都成立,
都成立, ![]()
![]() ,
,
得![]() ,有
,有![]() 或
或![]() .故存在最大的实数
.故存在最大的实数![]() 符合题意.
符合题意.

练习册系列答案
相关题目
 ,
, ,…,
,…, 的“倒平均数”为
的“倒平均数”为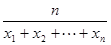 (
( ).已知数列
).已知数列 前
前 项的“倒平均数”为
项的“倒平均数”为 ,记
,记 (
( 与
与 的大小;
的大小; ,对(1)中的数列
,对(1)中的数列 ,是否存在实数
,是否存在实数 ,使得当
,使得当 时,
时, 对任意
对任意 满足
满足 ,
, (
( 且
且 ),
), (
(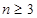 ),且
),且 的周期数列,设
的周期数列,设 为
为 .
. (n∈N*).已知数列{an}前n项的“倒平均数”为
(n∈N*).已知数列{an}前n项的“倒平均数”为 ,记cn=
,记cn= (n∈N*).
(n∈N*). Tn.
Tn.