题目内容
如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF=a(a>0),M是线段EF的中点.(1)求证:AC⊥BF;
(2)若二面角F-BD-A的大小为60°,求a的值;
(3)令a=1,设点P为一动点,若点P从M出发,沿棱按照M→E→C的路线运动到点C,求这一过程中形成的三棱锥P-BFD的体积的最小值.

【答案】分析:(1)建立空间直角坐标系,求出 ,即可证明AC⊥BF;
,即可证明AC⊥BF;
(2)求出平面ABD的法向量 ,利用
,利用 及二面角F-BD-A的大小为60°,求a的值;
及二面角F-BD-A的大小为60°,求a的值;
(3)解1a=1,设AC与BD交于O,则OF∥CM,所以CM∥平面FBD,当P点在M或C时,直接求出三棱锥P-BFD的体积的最小.
解2,求出 ,利用公式
,利用公式 ,求解即可.
,求解即可.
解答:解:建立空间坐标系,

(1)

 ,
,
所以AC⊥BF.(5分)
(2)平面ABD的法向量 ,
,
平面FBD的法向量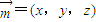


(3)解1设AC与BD交于O,则OF∥CM,所以CM∥平面FBD,
当P点在M或C时,三棱锥P-BFD的体积的最小.
 (14分)
(14分)
解2设AC与BD交于O,则OF∥CM,所以CM∥平面FBD,
当P点在M或C时,三棱锥P-BFD的体积的最小.
 ,
,
平面FBD的法向量
点C到平面FBD的距离
 .(14分)
.(14分)
点评:本题考查用空间向量求平面间的夹角,棱柱、棱锥、棱台的体积,向量语言表述线线的垂直、平行关系,考查空间想象能力,逻辑思维能力,是中档题.
 ,即可证明AC⊥BF;
,即可证明AC⊥BF;(2)求出平面ABD的法向量
 ,利用
,利用 及二面角F-BD-A的大小为60°,求a的值;
及二面角F-BD-A的大小为60°,求a的值;(3)解1a=1,设AC与BD交于O,则OF∥CM,所以CM∥平面FBD,当P点在M或C时,直接求出三棱锥P-BFD的体积的最小.
解2,求出
 ,利用公式
,利用公式 ,求解即可.
,求解即可.解答:解:建立空间坐标系,

(1)


 ,
,所以AC⊥BF.(5分)
(2)平面ABD的法向量
 ,
,平面FBD的法向量
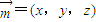


(3)解1设AC与BD交于O,则OF∥CM,所以CM∥平面FBD,
当P点在M或C时,三棱锥P-BFD的体积的最小.
 (14分)
(14分)解2设AC与BD交于O,则OF∥CM,所以CM∥平面FBD,
当P点在M或C时,三棱锥P-BFD的体积的最小.
 ,
,平面FBD的法向量

点C到平面FBD的距离

 .(14分)
.(14分)点评:本题考查用空间向量求平面间的夹角,棱柱、棱锥、棱台的体积,向量语言表述线线的垂直、平行关系,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,已知平行四边形ABCD所在平面外一点P,E、F分别是AB,PC的中点.求证:EF∥平面PAD.
如图,已知平行四边形ABCD所在平面外一点P,E、F分别是AB,PC的中点.求证:EF∥平面PAD. 如图,已知平行四边形ABCD中,AD=2,CD=
如图,已知平行四边形ABCD中,AD=2,CD= 如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF=
如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF= 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点. 如图,已知平行四边形ABCD中,AB=3,BC=2,∠BAD=60°,E为BC边上的中点,F为平行四边形内(包括边界)一动点,则
如图,已知平行四边形ABCD中,AB=3,BC=2,∠BAD=60°,E为BC边上的中点,F为平行四边形内(包括边界)一动点,则