题目内容
 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点.(Ⅰ)求证:GH∥平面CDE;
(Ⅱ)当四棱锥F-ABCD的体积取得最大值时,求平面ECF与平面ABCD所成锐二面角的余弦值.
分析:(Ⅰ)证明GH∥平面CDE,利用项目平行的判定,只需证明HG∥CD即可;
(Ⅱ)利用平面ADEF⊥平面ABCD,证明FA⊥平面ABCD,根据BD⊥CD,BC=2,CD=x,可求V(x)=
SABCD×FA=
x
(0<x<2),要使V(x)取得最大值,只须
(0<x<2)取得最大值,利用基本不等式可求.在平面DBC内过点D作DM⊥BC于M,连接EM,可得∠EMD是平面ECF与平面ABCD所成的二面角的平面角,由此可求平面ECF与平面ABCD所成的二面角的余弦值.
(Ⅱ)利用平面ADEF⊥平面ABCD,证明FA⊥平面ABCD,根据BD⊥CD,BC=2,CD=x,可求V(x)=
| 1 |
| 3 |
| 2 |
| 3 |
| 4-x2 |
| x2(4-x2) |
解答: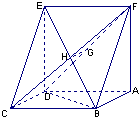 (Ⅰ)证明:∵EF∥AD,AD∥BC
(Ⅰ)证明:∵EF∥AD,AD∥BC
∴EF∥BC且EF=AD=BC
∴四边形EFBC是平行四边形
∴H为FC的中点-------------(2分)
又∵G是FD的中点,∴HG∥CD
∵HG?平面CDE,CD?平面CDE
∴GH∥平面CDE---------------------------------(4分)
(Ⅱ)解:∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,∴FA⊥平面ABCD.
∵BD⊥CD,BC=2,CD=x
∴FA=2,BD=
(0<x<2)------------(6分)
∴SABCD=CD•BD=x
∴V(x)=
SABCD×FA=
x
(0<x<2)------------(8分)
要使V(x)取得最大值,只须
(0<x<2)取得最大值,
∵
≤
=2,当且仅当x2=4-x2,即x=
时,V(x)取得最大值
在平面DBC内过点D作DM⊥BC于M,连接EM
∵BC⊥ED,∴BC⊥平面EMD,∴BC⊥EM
∴∠EMD是平面ECF与平面ABCD所成的二面角的平面角-------(10分)
∵当V(x)取得最大值时,CD=
,DB=
∴DM=
BC=1,EM=
∴sin∠EMD=
=
即平面ECF与平面ABCD所成的二面角的余弦值为
.------------------------------(12分)
 (Ⅰ)证明:∵EF∥AD,AD∥BC
(Ⅰ)证明:∵EF∥AD,AD∥BC∴EF∥BC且EF=AD=BC
∴四边形EFBC是平行四边形
∴H为FC的中点-------------(2分)
又∵G是FD的中点,∴HG∥CD
∵HG?平面CDE,CD?平面CDE
∴GH∥平面CDE---------------------------------(4分)
(Ⅱ)解:∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,∴FA⊥平面ABCD.
∵BD⊥CD,BC=2,CD=x
∴FA=2,BD=
| 4-x2 |
∴SABCD=CD•BD=x
| 4-x2 |
∴V(x)=
| 1 |
| 3 |
| 2 |
| 3 |
| 4-x2 |
要使V(x)取得最大值,只须
| x2(4-x2) |
∵
| x2(4-x2) |
| x2+(4-x2) |
| 2 |
| 2 |

在平面DBC内过点D作DM⊥BC于M,连接EM
∵BC⊥ED,∴BC⊥平面EMD,∴BC⊥EM
∴∠EMD是平面ECF与平面ABCD所成的二面角的平面角-------(10分)
∵当V(x)取得最大值时,CD=
| 2 |
| 2 |
∴DM=
| 1 |
| 2 |
| 5 |
∴sin∠EMD=
| ED |
| EM |
2
| ||
| 5 |
即平面ECF与平面ABCD所成的二面角的余弦值为
| ||
| 5 |
点评:本题考查线面平行,考查面面角,考查棱锥体积的计算,解题的关键是掌握线面平行的判定,正确作出面面角.

练习册系列答案
相关题目
 如图,已知平行四边形ABCD所在平面外一点P,E、F分别是AB,PC的中点.求证:EF∥平面PAD.
如图,已知平行四边形ABCD所在平面外一点P,E、F分别是AB,PC的中点.求证:EF∥平面PAD. 如图,已知平行四边形ABCD中,AD=2,CD=
如图,已知平行四边形ABCD中,AD=2,CD= 如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF=
如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,∠ADC=60°,AF= 如图,已知平行四边形ABCD中,AB=3,BC=2,∠BAD=60°,E为BC边上的中点,F为平行四边形内(包括边界)一动点,则
如图,已知平行四边形ABCD中,AB=3,BC=2,∠BAD=60°,E为BC边上的中点,F为平行四边形内(包括边界)一动点,则