题目内容
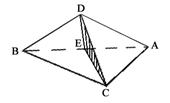
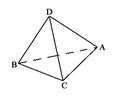
已知:AB与CD为异面直线,AC=BC,AD=BD.
求证:AB⊥CD.
求证:AB⊥CD.
说明:(1)应用判定定理,掌握线线垂直的一般思路.
(2)思路:欲证线线垂直,只需证线面垂直,再证线线垂直,而由已知构造线线垂直是关键.
(3)教学方法,引导学生分析等腰三角形三线合一的性质构造图形,找到证明方法.
证明:如图,取AB中点E,连结CE、DE
∵AC=BC,E为AB中点.
∴CE⊥AB
同理DE⊥AB,又CE∩DE=E,
且CE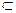 平面CDE,DE
平面CDE,DE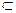 平面CDE.
平面CDE.
∴AB⊥平面CDE
又CD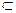 平面CDE
平面CDE
∴AB⊥CD.


(2)思路:欲证线线垂直,只需证线面垂直,再证线线垂直,而由已知构造线线垂直是关键.
(3)教学方法,引导学生分析等腰三角形三线合一的性质构造图形,找到证明方法.
证明:如图,取AB中点E,连结CE、DE
∵AC=BC,E为AB中点.
∴CE⊥AB
同理DE⊥AB,又CE∩DE=E,
且CE
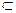 平面CDE,DE
平面CDE,DE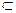 平面CDE.
平面CDE.∴AB⊥平面CDE
又CD
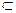 平面CDE
平面CDE∴AB⊥CD.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
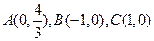 ,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。(Ⅰ)求点P的轨迹方程;(Ⅱ)若直线L经过
,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。(Ⅰ)求点P的轨迹方程;(Ⅱ)若直线L经过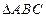 的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。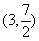
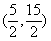
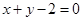 与x-7y-4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为( ).
与x-7y-4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为( ).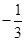
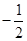
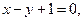 求
求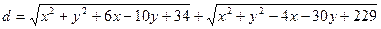 的最小值。
的最小值。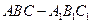 的各棱长都2,E,F分别是
的各棱长都2,E,F分别是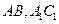 的中点,则EF的长是
的中点,则EF的长是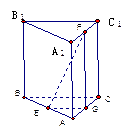



 中,点
中,点 ,
, 的中点为
的中点为 ,重心为
,重心为 ,则边
,则边 的长为( )
的长为( )


