题目内容
1.已知x,y∈{1,2,3,4,5,6},则使log2xy=1的概率为$\frac{1}{12}$.分析 通过log2xy=1可知y=2x,进而可知x=1且y=2或x=2且y=4或x=3且y=6,利用古典概型的概率计算公式计算即得结论.
解答 解:∵log2xy=1,
∴y=2x,
又∵x、y∈{1,2,3,4,5,6},
∴x=1且y=2或x=2且y=4或x=3且y=6,
∴所求概率P=$\frac{3}{6×6}$=$\frac{1}{12}$,
故答案为:$\frac{1}{12}$.
点评 本题考查古典概型,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.执行如图所示的程序框图,若输出b=3,则输入的实数a的取值范围是( )
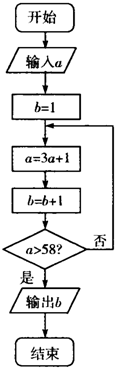

| A. | (19,+∞) | B. | (8,19] | C. | (6,19] | D. | ($\frac{5}{3}$,6] |
12.在△ABC中,b=3,c=8$\sqrt{3}$,∠A=$\frac{π}{6}$,则S△ABC=( )
| A. | 12$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 36 | D. | 18 |
6.若对?x,y∈[0,+∞),不等式ax-2≤ex+y-2+ex-y-2恒成立,则实数a的最大值是( )
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |