题目内容
设 是正实数,以下不等式
是正实数,以下不等式
① 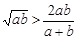 ,②
,② 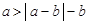 ,③
,③  ,④
,④  恒成立的序号为( )
恒成立的序号为( )
| A.①、③ | B.①、④ | C.②、③ | D.②、④ |
D
解析试题分析:∵ 是正实数,∴
是正实数,∴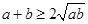 ,
, .当且仅当
.当且仅当 时取等号,∴①不恒成立;因为,
时取等号,∴①不恒成立;因为, ,所以,
,所以,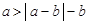 恒成立;由于
恒成立;由于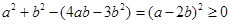 ,当
,当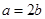 时,取等号,∴③不恒成立;由
时,取等号,∴③不恒成立;由 ,所以,
,所以, 恒成立,
恒成立,
故选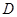 .
.
考点:基本不等式

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
设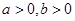 ,若
,若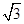 是
是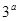 与
与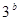 的等比中项,则
的等比中项,则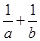 的最小值为( )
的最小值为( )
| A.8 | B.4 | C.1 | D.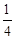 |
设正实数x,y,z满足x2-3xy+9y2-z=0,则当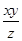 取得最大值时,
取得最大值时,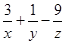 的最大值为( )
的最大值为( )
| A.1 | B.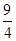 | C.-1 | D.3 |
设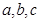 都是正实数,且
都是正实数,且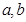 满足
满足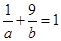 ,则使
,则使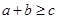 恒成立的
恒成立的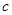 的范围是( )
的范围是( )
| A.(0,8] | B.(0,10] | C.(0,12] | D.(0,16] |
函数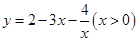 的最大值是( )
的最大值是( )
A.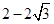 | B.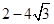 | C.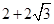 | D.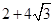 |
设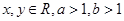 ,若
,若 ,则
,则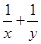 的最大值为( )
的最大值为( )
| A.2 | B.3 | C.4 | D.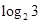 |
若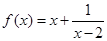
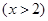 在
在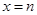 处取得最小值,则
处取得最小值,则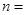 ( )
( )
A.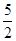 | B.3 | C.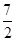 | D.4 |
已知点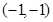 在直线
在直线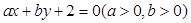 上,则
上,则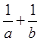 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
已知 ,函数
,函数 的最小值是 ( )
的最小值是 ( )
| A.5 | B.4 | C.8 | D.6 |